Prim算法

发表于 | 分类于

引言

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克发现；并在1957年由美国计算机科学家罗伯特·普里姆独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

1.最小生成树

对于具有n个顶点的连通图的生成树，它包含了该连通图的全部n个顶点，但仅包含其n-1条边。需要注意的是，生成树中不具有回路。

如果连通图是一个网络，则其生成树中的边也带权，且该网络的所有带权生成树中权值总和最小的生成树为最小生成树(也称为最小代价生成树).

一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和。广义上而言，对于非连通无向图来说，它的每一连通分量同样有最小生成树。
以有线电视电缆的架设为例，若只能沿着街道布线，则以街道为边，而路口为顶点，其中必然有一最小生成树能使布线成本最低.

如下的两个生成树都是典型的最小生成树:

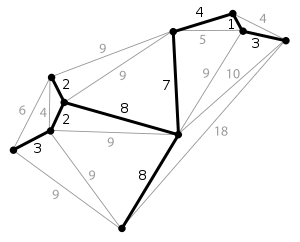
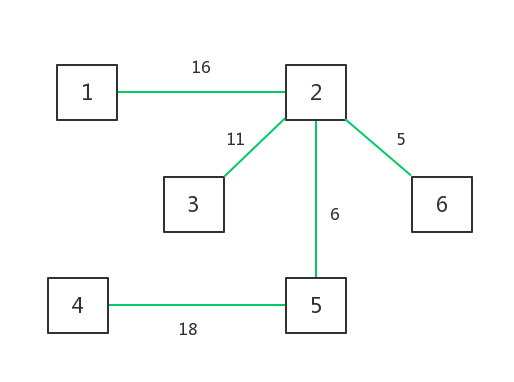
2.Prim算法

1)基本思想

对于图G而言，V是所有顶点的集合；现在，设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。 从所有uЄU，vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v)，将顶点v加入集合U中，将边(u, v)加入集合T中，如此不断重复，直到U=V为止，最小生成树构造完毕，这时集合T中包含了最小生成树中的所有边。

2)示例

如下是一个典型的通过Prim算法获取最小生成树的过程:

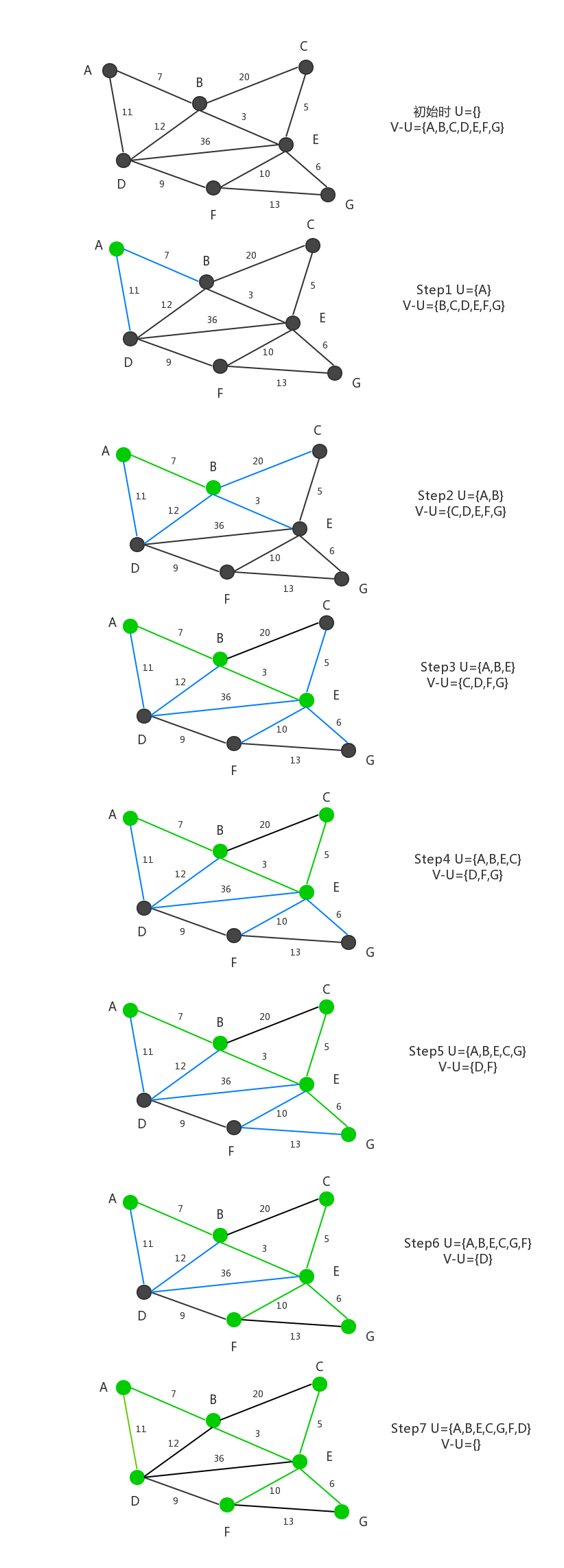
3)算法实现

在实现邻接矩阵和邻接表的Prim算法之前，我们先看一个思想来自维基的实现,它的好处是非常直观，后面两种实现都是来自于这种实现的思想:

它的顶点和边的定义为: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Vertex<T> {
    T key;
    public Vertex(T key){
        this.key=key;
    }
}
public class Edge<T> {
    Vertex<T>start;
    Vertex<T>end;
    int weight;
    public Edge(Vertex<T>start,Vertex<T>end,int weight){
        this.start=start;
        this.end=end;
        this.weight=weight;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
private static void buildGraph(List<Vertex<String>>vertexList,
                                   List<Edge<String>>edgeList){
        Vertex<String> v1=new Vertex<>("A");
        vertexList.add(v1);
        Vertex<String>v2=new Vertex<>("B");
        vertexList.add(v2);
        Vertex<String>v3=new Vertex<>("C");
        vertexList.add(v3);
        Vertex<String>v4=new Vertex<>("D");
        vertexList.add(v4);
        Vertex<String>v5=new Vertex<>("E");
        vertexList.add(v5);
        Vertex<String>v6=new Vertex<>("F");
        vertexList.add(v6);
        Vertex<String>v7=new Vertex<>("G");
        vertexList.add(v7);
        //边AB
        edgeList.add(new Edge<>(v1,v2,7));
        //边BC
        edgeList.add(new Edge<>(v2,v3,20));
        //边AD
        edgeList.add(new Edge<>(v1,v4,11));
        //边BD
        edgeList.add(new Edge<>(v2,v4,12));
        //边BE
        edgeList.add(new Edge<>(v2,v5,3));
        //边CE
        edgeList.add(new Edge<>(v3,v5,5));
        //边DE
        edgeList.add(new Edge<>(v4,v5,36));
        //边DF
        edgeList.add(new Edge<>(v4,v6,9));
        //边EF
        edgeList.add(new Edge<>(v5,v6,10));
        //边EG
        edgeList.add(new Edge<>(v5,v7,6));
        //边FG
        edgeList.add(new Edge<>(v6,v7,13));
    }
    private static <T> void addEdge(List<Edge<T>>edgeList,Vertex<T>start,Vertex<T>end,int weight){
        edgeList.add(new Edge<T>(start,end,weight));
    }
    public static final int MAX_VALUE=Integer.MAX_VALUE;
    public static void prim(){
        List<Vertex<String>>vertexList=new ArrayList<>();
        List<Edge<String>>edgeList=new ArrayList<>();
        List<Vertex<String>>visitVerList=new ArrayList<>();
        //visitEdgeList is just the result of prim tree
        List<Edge<String>>visitEdgeList=new ArrayList<>();
        buildGraph(vertexList,edgeList);
        Vertex<String>startVer=vertexList.get(0);
        visitVerList.add(startVer);
        for(int i=0;i<vertexList.size();++i){
            Vertex<String>tempVer=new Vertex<>(startVer.key);
            Edge<String>tempEdge=new Edge<>(startVer,startVer,MAX_VALUE);
            for(Vertex<String>ver:visitVerList){
                for(Edge<String>edge:edgeList){
                    if(edge.start==ver&&!containVertex(visitVerList,edge.end)){
                       if(edge.weight<tempEdge.weight){
                           tempVer=edge.end;
                           tempEdge=edge;
                       }
                    }
                }
            }
            visitVerList.add(tempVer);
            visitEdgeList.add(tempEdge);
        }
        printEdges(edgeList);
    }

由于图既可采用邻接矩阵存储，也可采用邻接表存储，故这里给出邻接矩阵和邻接表的算法实现.

首先是邻接矩阵的Prim算法实现。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
static class Vertex<T>{
        int pos;
        T key;
        public Vertex(int pos,T key){
            this.pos=pos;
            this.key=key;
        }
    }
    
    static class Edge<T>{
        Vertex<T> start;
        Vertex<T> end;
        int weight;
        public Edge(Vertex<T> start,Vertex<T> end,int weight){
            this.start=start;
            this.end=end;
            this.weight=weight;
        }
    }
    
    private static <T> int getClosestVertexPos(Vertex<T>sourceVer,int[][]adjArray){
        int k=-1;
        int minWeight=adjArray[sourceVer.pos][0];
        for(int j=1;j<adjArray.length;++j){
            if(j==sourceVer.pos||adjArray[sourceVer.pos][j]==VISITED_FLAG_VALUE){
                continue;
            }
            if(adjArray[sourceVer.pos][j]<minWeight){
                minWeight=adjArray[sourceVer.pos][j];
                k=j;
            }
        }
        return k;
    }
    
    public static <T> List<Edge<T>> prim(Vertex<T>[]vertexArray,int[][]adjArray){
        //actually start could be random between 0 and vertexArray.length
        int start=0;
        List<Vertex<T>> primVertexList=new ArrayList<>();
        List<Edge<T>>primEdgeList=new ArrayList<>();
        primVertexList.add(vertexArray[start]);
        while(primVertexList.size()<vertexArray.length){
          
            List<Edge<T>>minEdgeList=new ArrayList<>();
            for(Vertex<T>ver:primVertexList){
                int k=getClosestVertexPos(ver,adjArray);
                if(k!=-1){
                    minEdgeList.add(new Edge<T>(ver,vertexArray[k],adjArray[ver.pos][k]));
                    //adjArray[ver.pos][k]=VISITED_FLAG_VALUE;
                }
            }
            
            if(minEdgeList.isEmpty()){
                break;
            }
            
            int minWeight=minEdgeList.get(0).weight;
            Edge<T>minEdge=minEdgeList.get(0);
            for(Edge<T>edge:minEdgeList){
                if(edge.weight<minWeight){
                    minWeight=edge.weight;
                    minEdge=edge;
                }
            }
            
            primVertexList.add(minEdge.end);
            primEdgeList.add(minEdge);
            adjArray[minEdge.start.pos][minEdge.end.pos]=VISITED_FLAG_VALUE;
            
        }
        
        return primEdgeList;
    }

这是使用邻接表来实现Prim算法的代码: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
static class PrimVertex<T>{
    int pos;
    T data;
    public PrimVertex(int pos,T data){
        this.pos=pos;
        this.data=data;
    }
}
static class PrimEdge<T>{
    PrimVertex<T>start;
    PrimVertex<T>end;
    int weight;
    public PrimEdge(PrimVertex<T>start,PrimVertex<T>end,int weight){
        this.start=start;
        this.end=end;
        this.weight=weight;
    }
}
public static <T> List<PrimEdge<T>> prim(Vertex<T>[]graph){
    if(null==graph){
        return null;
    }
    List<PrimVertex<T>>visitVertexList=new ArrayList<>();
    List<PrimEdge<T>>visitEdgeList=new ArrayList<>();
    visitVertexList.add(new PrimVertex<>(0,graph[0].data));
    while(visitVertexList.size()<graph.length){
        List<PrimEdge<T>>minEdgeList=getMinEdgeList(graph,visitVertexList,visitEdgeList);
        if(null==minEdgeList||minEdgeList.isEmpty()){
            break;
        }
        PrimEdge<T>minEdge=minEdgeList.get(0);
        for(PrimEdge<T>edge:minEdgeList){
            if(edge.weight<minEdge.weight){
                minEdge=edge;
            }
        }
        visitVertexList.add(minEdge.end);
        visitEdgeList.add(minEdge);
    }
    
    return visitEdgeList;
    
}
private static <T> List<PrimEdge<T>>getMinEdgeList(Vertex<T>[]graph,List<PrimVertex<T>>visitedVertexList,
                                                   List<PrimEdge<T>>visitedEdgeList){
    List<PrimEdge<T>>minEdgeList=new ArrayList<>();
    for(PrimVertex<T>ver:visitedVertexList){
        PrimEdge<T>edge=getMinEdge(graph,ver,visitedVertexList);
        if(null!=edge){
            minEdgeList.add(edge);
        }
    }
    return minEdgeList;
}
private static <T> PrimEdge<T>getMinEdge(Vertex<T>[]graph,PrimVertex<T>ver,List<PrimVertex<T>>visitedVertexList){
    if(null==ver){
        return null;
    }
    Edge tempEdge=graph[ver.pos].edgeLink;
    if(null==tempEdge){
        return null;
    }
    Edge minEdge=tempEdge;
    while(tempEdge.next!=null){
        if(tempEdge.weight<minEdge.weight&&!containsVer(tempEdge.adjVexPos,visitedVertexList)){
            minEdge=tempEdge;
        }
        tempEdge=tempEdge.next;
    }
    
    if(containsVer(minEdge.adjVexPos,visitedVertexList)){
        return null;
    }
    return new PrimEdge<>(ver,new PrimVertex<>(tempEdge.adjVexPos,graph[tempEdge.adjVexPos].data),tempEdge.weight);
    
}
private static <T> boolean containsVer(int pos,List<PrimVertex<T>>visitedVertexList){
    for(PrimVertex<T>ver:visitedVertexList){
        if(ver.pos==pos){
            return true;
        }
    }
    return false;
}