Kruskal算法

发表于 | 分类于

引言

Kruskal算法是一种用来查找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

1.算法思想及示例

Kruskal算法的思想非常简单:按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。显然该算法的难点在于判断是否构成回路。

如下图显示了Kruskal算法的过程:

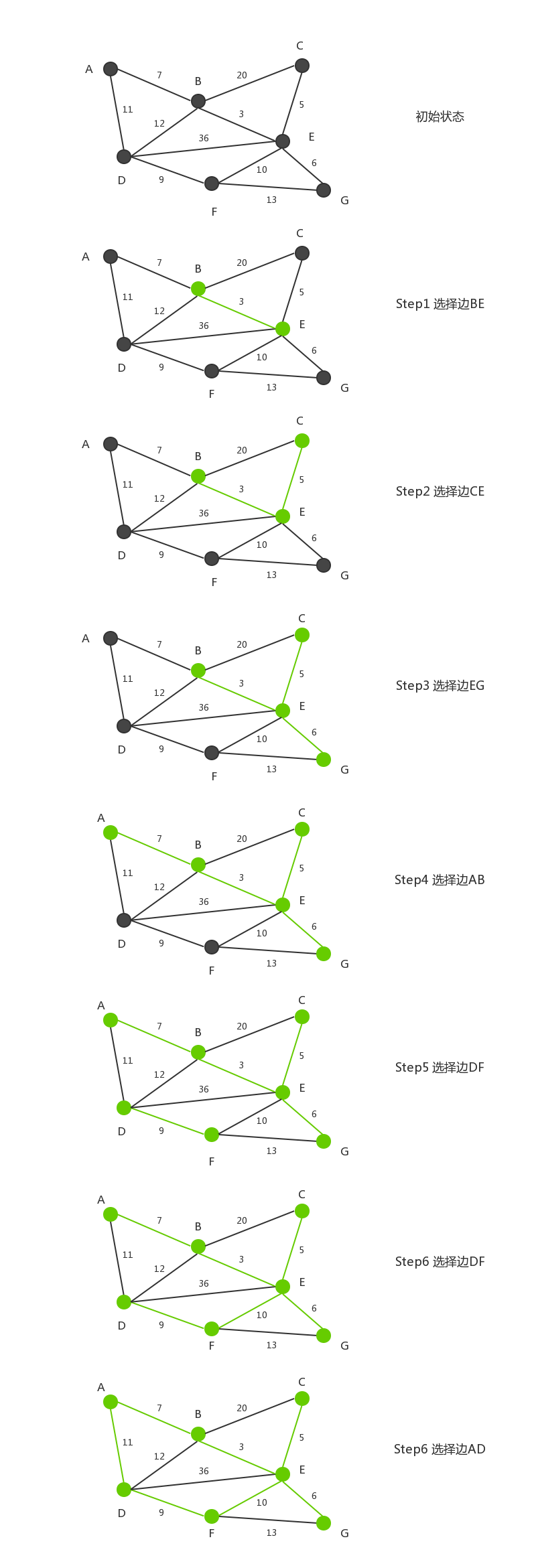
2.算法实现

根据前面介绍的克鲁斯卡尔算法的基本思想和做法，我们能够了解到，克鲁斯卡尔算法重点需要解决的以下两个问题：

  • 1) 对图的所有边按照权值大小进行排序。
  • 2) 将边添加到最小生成树中时，怎么样判断是否形成了回路。

问题一很好解决，采用排序算法进行排序即可。

问题二，有两种处理方式，第一种很简单，就是判断待加入的边的两个顶点是否在已加入的边上，如果都在，则会构成回路,否则不会;

第二种处理方式是：记录顶点在”最小生成树”中的终点，顶点的终点是”在最小生成树中与它连通的最大顶点”。然后每次需要将一条边添加到最小生存树时，判断该边的两个顶点的终点是否重合，重合的话则会构成回路。以下图来进行说明： 

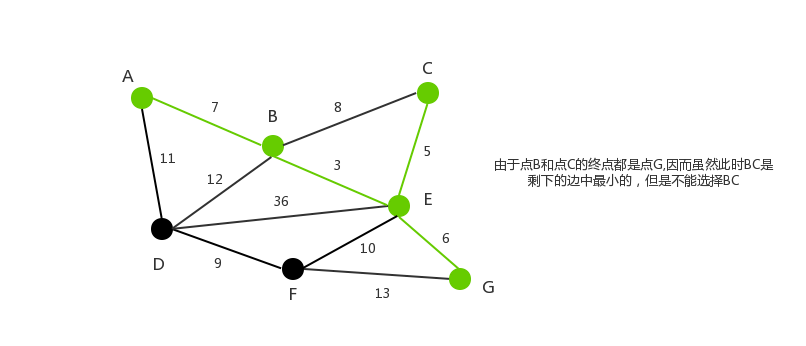
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public class Edge<T> implements Comparable<Edge<T>> {
    Vertex<T>start;
    Vertex<T>end;
    int weight;
    public Edge(Vertex<T>start,Vertex<T>end,int weight){
        this.start=start;
        this.end=end;
        this.weight=weight;
    }
    @Override
    public int compareTo(Edge<T> another) {
        return weight-another.weight;
    }
}
  public static <T> List<Edge<T>>kruskal(Graph<T> graph){
        if(null==graph){
            return null;
        }
        //sort edges first
        Collections.sort(graph.edgeList);
        //then add edges
        List<Edge<T>>kruskalList=new ArrayList<>();
        for(Edge<T>edge:graph.edgeList){
            if(kruskalList.size()==graph.vertexList.size()-1){
                break;
            }
            if(!willBuildCircle(edge,kruskalList)){
                kruskalList.add(edge);
            }
        }
        return kruskalList;
    }
    private static <T> boolean willBuildCircle(Edge<T>edge,List<Edge<T>>currentEdgeList){
        if(null==edge||null==currentEdgeList||currentEdgeList.isEmpty()){
            return false;
        }
        for(Edge<T>temp:currentEdgeList){
            if(temp.start==edge.start&&temp.end==edge.end){
                return true;
            }else if(temp.start==edge.end&&temp.end==edge.start){
                return true;
            }
        }
        return false;
    }