Dijkstra算法

发表于 | 分类于

引言

Dijkstra算法是由荷兰计算机科学家艾兹赫尔·戴克斯特拉提出。Dijkstra算法使用了广度优先搜索解决非负权有向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。举例来说，如果图中的顶点表示城市，而边上的权重表示城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径。

1.基本思想及示例

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。
此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。
然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。

如下是求图中顶点G到其它各顶点最短路径的示例:

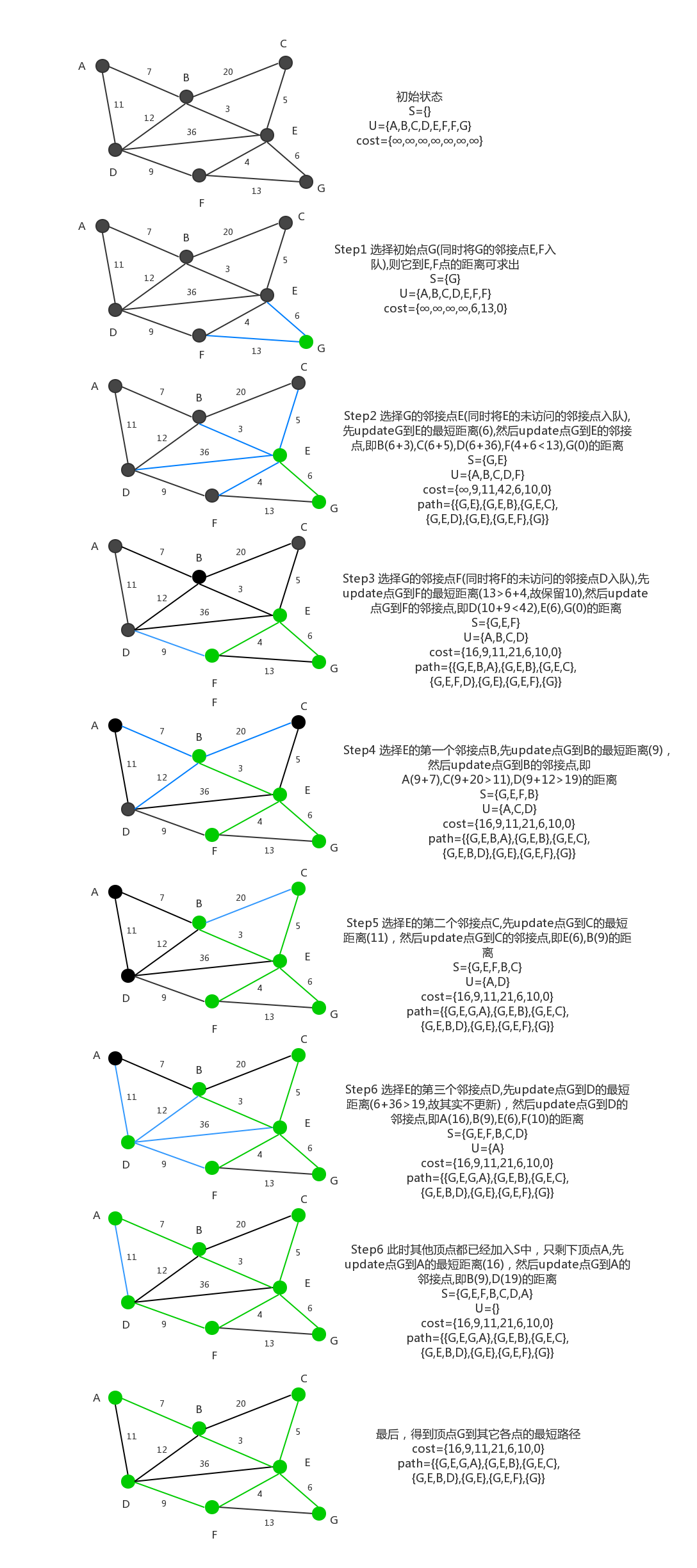
2.算法实现

其实算法的实现非常简单，就是在BFS的时候进行最短路径的比较和更新。

如下是使用邻接表的算法实现: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class Vertex<T> {
    //this is very important in Dijkstra algorithm
    public int pos;
    public T data;
    //该顶点指向的第一条边
    public Edge edgeLink;
}
public static <T> List<Vertex<T>>[]dijkstra(Vertex<T>[]graph,T item){
        if(null==graph||null==item){
            return null;
        }
        List<Vertex<T>>[]path=new List[graph.length];
        int[]costArray=new int[graph.length];
        int[]visitedArray=new int[graph.length];
        Vertex<T>startVer=null;
        for(int i=0;i<graph.length;++i){
            path[i]=new ArrayList<>();
            if(graph[i].data.equals(item)){
                costArray[i]=0;
                visitedArray[i]=1;
                path[i].add(graph[i]);
                startVer=graph[i];
            }else{
                costArray[i]=Integer.MAX_VALUE;
                visitedArray[i]=0;
            }
        }
        if(null==startVer){
            Log.d(TAG,"not found item in graph");
            return null;
        }
        Queue<Vertex<T>>verQueue=new LinkedBlockingDeque<>(5);
        verQueue.offer(startVer);
        while(!verQueue.isEmpty()){
            Vertex<T>currentVer=verQueue.poll();
            Edge edge=currentVer.edgeLink;
            while(edge!=null){
                if(visitedArray[edge.adjVexPos]==0){
                    verQueue.offer(graph[edge.adjVexPos]);
                    visitedArray[edge.adjVexPos]=1;
                    //要注意溢出
                    if(costArray[currentVer.pos]+edge.weight<costArray[edge.adjVexPos]){
                        costArray[edge.adjVexPos]=costArray[currentVer.pos]+edge.weight;
                        path[edge.adjVexPos].add(graph[edge.adjVexPos]);
                    }
                }
                edge=edge.next;
            }
        }
        return path;
    }