二叉树常用操作的Java实现

发表于 | 分类于

引言

二叉树的Java实现

之前有两篇博客是利用C++实现了二叉树的各种常用操作，这里提供二叉树常用操作的Java实现。
其实如果不追求空间最小，那么就不必非要采用数组实现，而是直接利用Java中的Stack去实现。只要利用Stack后进先出的特性，就可以很好地实现各种非递归算法。

1.二叉树节点的定义

考虑到拓展性，当然要使用范型来定义。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class BinaryNode<T>{
	
	public T data;
	public BinaryNode<T>left;
	public BinaryNode<T>right;
	public BinaryNode(T data){
	   this.data=data;
	}
	public BinaryNode(T data,BinaryNode<T>left,BinaryNode<T>right){
        
        this.data=data;
        this.left=left;
        this.right=right;   
	}
}

2.二叉树的创建

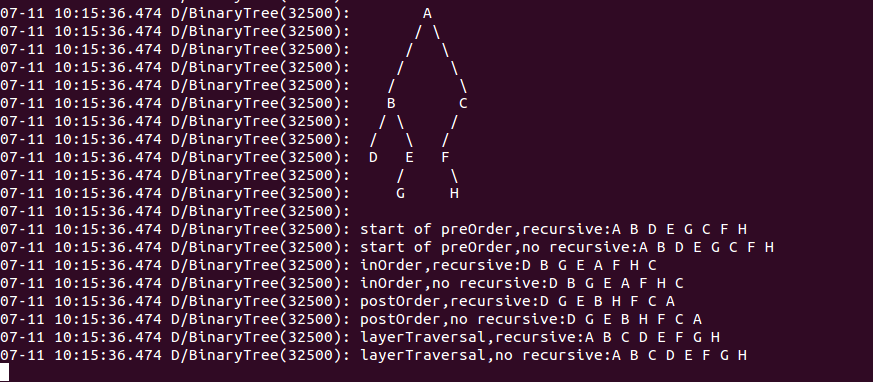
下面提供一个利用广义表创建二叉树的方法,比如利用”A(B(D,E(G)),C(F(,H)))”创建二叉树. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public static BinaryNode<Character>createBTreeByGeneralList(Character[]charArray){
  BinaryNode<Character>root=null;
  BinaryNode<Character>currentNode=null;
  Stack<BinaryNode<Character>>stack=new Stack();
  boolean leftFlag=true;
  for(Character c:charArray){
     switch(c){
        case '(':
             stack.push(currentNode);
             leftFlag=true;
             break;
        case ')':
              stack.pop();
              break;
        case ',':
               leftFlag=false;
               break;
        default:
               currentNode=new BinaryNode<>(c);
               if(root==null){
                   root=currentNode;
               }else if(leftFlag){
                   stack.peek().left=currentNode;
               }else{
                   stack.peek().right=currentNode;
               }               
     }
  }
  return root; 
}

为了进行测试，在StackOverflow中找到一个可以打印出二叉树形状的方法，如下所示： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
///////////////////////start of print binary tree as tree shape/////////////////
public static <T> void printAsHorizontalTreeShape(BinaryNode<T>root){
    int maxLevel=maxDepth(root,true);
    Log.d(TAG,"maxLevel:"+maxLevel);
    print("\n");
    printNodes(Collections.singletonList(root),1,maxLevel);
}
private static <T> void printNodes(List<BinaryNode<T>>nodeList,int level,int maxLevel){
   if(null==nodeList||nodeList.isEmpty()||isAllElementsNull(nodeList)){
       return;
   }
    int floor=maxLevel-level;
    int edgeLines=(int)(Math.pow(2,(Math.max(floor-1,0))));
    int firstSpaces=(int)Math.pow(2,floor)-1;
    int betweenSpaces=(int)Math.pow(2,floor+1)-1;
    printWhiteSpaces(firstSpaces);
    List<BinaryNode<T>>newNodes=new ArrayList<>();
    for(BinaryNode<T> node:nodeList){
        if(node!=null){
            print(node.data.toString());
            newNodes.add(node.left);
            newNodes.add(node.right);
        }else{
            newNodes.add(null);
            newNodes.add(null);
            print(" ");
        }
        printWhiteSpaces(betweenSpaces);
    }
    print("\n");
    for(int i=1;i<=edgeLines;++i){
        for(int j=0;j<nodeList.size();++j){
            printWhiteSpaces(firstSpaces-i);
            if(nodeList.get(j)==null){
                printWhiteSpaces(edgeLines+edgeLines+i+1);
                continue;
            }
            if(nodeList.get(j).left!=null){
                print("/");
            }else{
                printWhiteSpaces(1);
            }
            printWhiteSpaces(i+i-1);
            if(nodeList.get(j).right!=null){
                print("\\");
            }else{
                printWhiteSpaces(1);
            }
            printWhiteSpaces(edgeLines+edgeLines-i);
        }
        print("\n");
    }
    printNodes(newNodes,level+1,maxLevel);
}
public static <T> boolean isAllElementsNull(List<T>list){
    for(T t:list){
        if(t!=null){
            return false;
        }
    }
    return true;
}
public static void printWhiteSpaces(int count){
    for(int i=0;i<count;++i){
        print(" ");
    }
}

测试依据广义表创建二叉树的代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
public static BinaryNode<Character> testCreation(){
	
    char[]array="A(B(D,E(G)),C(F(,H))".toCharArray();
    Character[]arr=new Character[array.length];
    for(int i=0;i<array.length;++i){
       arr[i]=array[i];
    }
    BinaryNode<Character>root=BinaryTree.createBTreeByGeneralList(arra);
    BinaryTree.printAsHorizontalTreeShape(root);
}

结果如下：

3.前序遍历

所谓前充遍历，就是最先访问根结点，之后是左子结点，最后是右子结点。
递归算法太简单，就不多说了。对于非递归算法 ，由于是先访问左子结点，后访问右子结点，而Stack的规则是先进后出，所以只要让右子节点先进入Stack即可。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public static <T> void preOrderTraversal(BinaryNode<T>root,boolean recursionFlag){
	if(recursionFlag){
       if(null==root){
           return;
       }
       print(root.data.toString()+" ");
       preOrderTraversal(root.left,true);
       preOrderTraversal(root.right,true); 
	}else{
	   if(null==root){
	      return;
	   }
       BinaryNode<T>currentNode;
       Stack<BinaryNode<T>>stack=new Stack<>();
       stack.push(root);
       while(!stack.isEmpty()){
          currentNode=stack.pop();
          print(currentNode.data.toString()+" ");
          //push right child into stack first, so it will be poped later than left child
          if(null!=currentNode.right){
              stack.push(currentNode.right);
          }
          if(null!=currentNode.left){
              stack.push(currentNode.left);
          } 
       }  
	}
}

4.中序遍历

所谓中序遍历，即结点的访问顺序为：左孩子–>根结点–>右孩子。
递归算法也是极为简单，不提也罢。对于非递归算法，由于需要先遍历左孩子，为了达到这个目的，就需要借助另一个Stack的帮助，以记录这是第几次访问当前结点，如果是第一次，就需要仍然把它放回去，并且将它的左孩子push进入stack,当然，此时对应stack中的标记也要修改。如果是第二次，则可以打印它，并且将它的右孩子(如果存在)加入到Stack中。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public static final int FLAG_FIRST=1;
public static final int FLAG_SECOND=2;
public static final int FLAG_THIRD=3;
public static <T> void inOrderTraversal(BinaryNode<T>root,boolean recursionFlag){
	 if(recursionFlag){
	     if(null==root){
	        return;
	     }
	     inOrderTraversal(root.left,true);
	     print(root.data.toString()+" ");
	     inOrderTraversal(root.right,true);
	 }else{
	    if(null==root){
	       return;
	    }
	    BinaryNode<T>currentNode;
	    Stack<BinaryNode<T>>nodeStack=new Stack<>();
	    Stack<Integer>flagStack=new Stack<>();
        nodeStack.push(root);
        flagStack.push(FLAG_FIRST);
        while(!stack.isEmpty()){
           currentNode=nodeStack.peek();
           if(flagStack.peek()==FLAG_FIRST){
              flagStack.pop();
              flagStack.push(FLAG_SECOND);
              //因为有flagStack的帮助，所以这里需要先将左孩子而不是右孩子push进入nodeStack
              if(currentNode.left!=null){
                  nodeStack.push(currentNode.left);
                  flagStack.push(FLAG_FIRST);
              }
           }else{
               print(currentNode.data.toString()+" "); 
               nodeStack.pop();
               flagStack.pop();
               if(null!=currentNode.right){
                  nodeStack.push(currentNode.right);
                  flagStack.push(FLAG_FIRST);
               }
           }
        } 
	 }
}

5.后序遍历

后序遍历的结点遍历顺序为:左孩子–>右孩子–>根结点.
类似地，对于非递归算法，仍然需要符号Stack的帮助，并且要进行再次判断，如果是第一次访问到这个结点，则暂时不能打印它，而是要将它的左孩子push到Stack中，当然，flagStack中的标记也要相应改变;如果是第二次访问到这个结点，则仍然还不能打印它，而是要将它的右孩子push到Stack中，同时flagStack要相应地改变。

只有第三次访问到这个节点，才能打印它。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public static <T> void postOrderTraversal(BinaryNode<T>root,boolean recursionFlag){
	
	if(recursionFlag){
	   if(null==root){
	      return;
	   }
	   postOrderTraversal(root.left,true);
	   postOrderTraversal(root.right,true);
	   print(root.data.toString()+" ");
	}else{
	   if(null==root){
	      return;
	   }
	   Stack<BinaryNode<T>>nodeStack=new Stack<>();
	   Stack<Integer>flagStack=new Stack<>();
	   BinaryNode<T>currentNode;
	   int flag;
	   nodeStack.push(root);
	   flagStack.push(FLAG_FIRST);
	   while(!nodeStack.isEmpty()){
	      currentNode=nodeStack.peek();
          flag=flagStack.peek();
          if(flag==FLAG_STACK){
             flagStack.pop();
             flagStack.push(FLAG_SECOND);
             if(null!=currentNode.left){
                nodeStack.push(currentNode.left);
                flagStack.push(FLAG_FIRST);
             }
          }else if(flag==FLAG_SECOND){
              flagStack.pop();
              flagStack.push(FLAG_THIRD);
              if(null!=currentNode.right){
                  nodeStack.push(currentNode.right);
                  flagStack.push(FLAG_FIRST);
              }
          }else{
              print(currentNode.data.toString()+" ");
              nodeStack.pop();
              flagStack.pop();
          }  
	   }
	}
}

6.层次遍历

层次遍历其实就是严格按照FIFO的顺序进行遍历，所以需要使用队列.
Java中入队方法是Queue.offer();出队方法是Queue.poll(); 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public static <T> void layerTraversal(BinaryNode<T>root,boolean recursionFlag){
    if(recursionFlag){
    	if(null==root){
    		return;
    	}
    	Queue<BinaryNode<T>>nodeQueue=new LinkedBlockingDeque<>(15);
    	nodeQueue.offer(root);
    	recursiveLayerTraversal(nodeQueue);
    }else{
    	if(null==root){
    		return;
    	}
    	Queuey<BinaryNode<T>>nodeQueue=new LinkedBlockingDeque<>(15);
    	nodeQueue.offer(root);
    	BinaryNode<T>currentNode;
    	while(!nodeQueue.isEmpty()){
            currentNode=nodeQueue.poll();
            print(currentNode.data.toString()+" ");
            if(currentNode.left!=null){
            	nodeQueue.offer(currentNode.left);
            }
            if(currentNode.right!=null){
            	nodeQueue.offer(currentNode.right);
            }
    	}
    }
}
private static <T> void recursiveLayerTraversal(Queue<BinaryNode<T>>nodeQueue){
	if(nodeQueue.isEmpty()){
		return;
	}
	BinaryNode<T>currentNode=nodeQueue.poll();
	if(null==currentNode){
		return;
	}
	print(currentNode.data.toString()+" ");
	if(currentNode.left!=null){
		nodeQueue.offer(currentNode.left);
	}
	if(currentNode.right!=null){
		nodeQueue.offer(currentNode.right);
	}
	recursiveLayerTraversal(nodeQueue);
}

需要注意的是,左孩子和右孩子进入队列的顺序可调换.

7.求二叉树深度

其实求深度很简单，只要采用某种方式遍历即可，此处采用最简单的前序遍历.此处定义根节点深度为1,依次往下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public static <T> int getDepth(BinaryNode<T>rootNode,boolean recursionFlag){
	if(recursionFlag){
		if(null==rootNode){
			return 0;
		}
		int leftHeight=getDepth(rootNode.left,true)+1;
		int rightHeight=getDepth(rootNode.right,true)+1;
		return leftHeight>rightHeight?leftHeight:rightHeight;
	}else{
		if(null==rootNode){
			return 0;
		}
		BinaryNode<T>currentNode;
		int currentDepth=0,maxDepth=0;
		Stack<BinaryNode<T>>nodeStack=new Stack<>();
		Stack<Integer>depthStack=new Stack<>();
		nodeStack.push(rootNode);
		depthStack.push(1);
		while(!nodeStack.isEmpty()){
			currentNode=nodeStack.pop();
			currentDepth=depthStack.pop();
            if(currentDepth>maxDepth){
            	maxDepth=currentDepth;
            }
            //其实此处左孩子和右孩子哪个先入栈都行
            if(currentNode.right!=null){
            	nodeStack.push(currentNode.right);
            	depthStack.push(currentDepth+1);
            }
            if(currentNode.left!=null){
            	nodeStack.push(currentNode.left);
            	depthStack.push(currentDepth+1);
            }
		}
		return maxDepth;
	}
}

8.遍历测试

利用之前创建的二叉树进行各种遍历方式的测试，测试代码如下所示: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
BinaryTree.print("start of preOrder,recursive:");
BinaryTree.preOrderTraversal(root,true);
BinaryTree.print("\nstart of preOrder,no recursive:");
BinaryTree.preOrderTraversal(root,false);
BinaryTree.print("\ninOrder,recursive:");
BinaryTree.inOrderTraversal(root,true);
BinaryTree.print("\ninOrder,no recursive:");
BinaryTree.inOrderTraversal(root,false);
BinaryTree.print("\npostOrder,recursive:");
BinaryTree.postOrderTraversal(root,true);
BinaryTree.print("\npostOrder,no recursive:");
BinaryTree.postOrderTraversal(root,false);
BinaryTree.print("\nlayerTraversal,recursive:");
BinaryTree.layerTraversal(root,true);
BinaryTree.print("\nlayerTraversal,no recursive:");
BinaryTree.layerTraversal(root,false);

结果如下所示: