平衡二叉树及Java实现

发表于 | 分类于

引言

前面一篇博客中我们讲到二叉查找树的评价查找效率可达到O(logN)，但是它在最坏情况下的查找效率可能退化为O(N),如下所示:

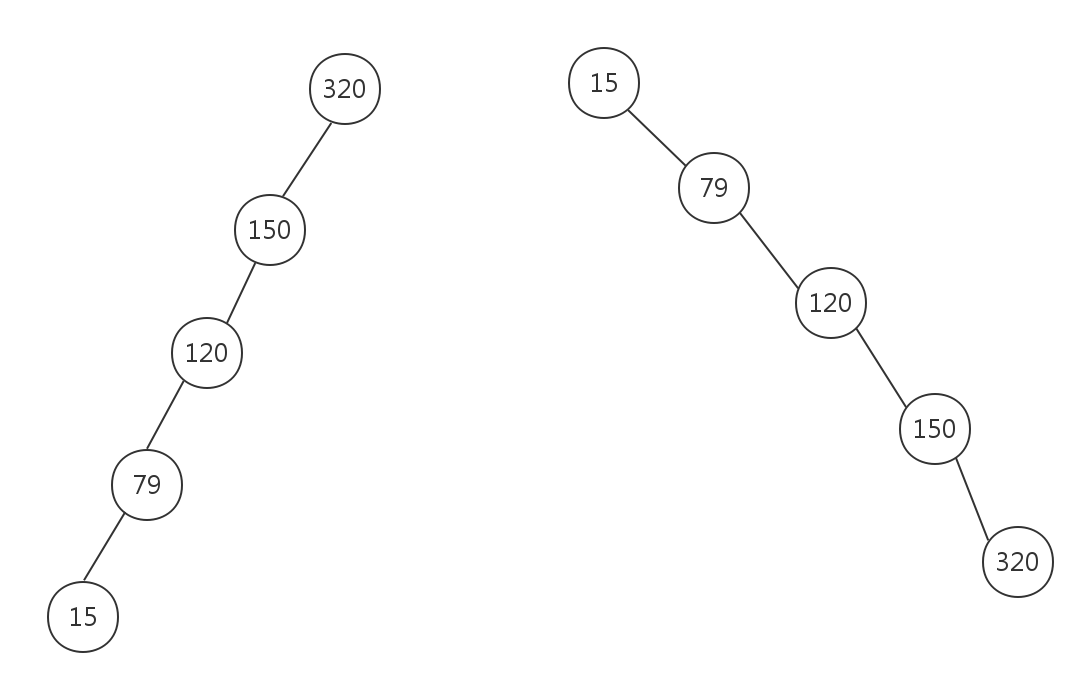
显然此时二叉查找树已经退化为链表,从而查找效率低下.

为了解决这个问题,有许多的前辈做了无数的优化工作,核心思想都是保持二叉树的平衡或者基本平衡,主要的成果为平衡二叉树(AVL),红黑树,Treap树,伸展树(Splay Tree).
今天先介绍基础的平衡二叉树,理解了它,有助于理解其他的优化方式.

ps:维基等将平衡二叉树定义为一大类，包括AVL树,红黑树,Treap树等。而大陆的书本中平衡二叉树比较狭义，仅仅指AVL树。我个人倾向于维基的定义.

1.AVL的定义

AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O（log n）。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

AVL节点的定义如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class AVLNode<T>{
	public T data;
	public AVLNode<T>left;
	public AVLNode<T>right;
	public int height;
	public AVLNode(T data){
		this(data,0,null,null);
	}
	public AVLNode(T data,int height,AVLNode<T>left,AVLNode<T>right){
		this.data=data;
		this.height=height;
		this.left=left;
		this.right=right;
	}
}

可见,相比之前的BinaryNode,多了一个height字段.其中高度的定义和深度的定义恰好相反：空节点是-1，叶子节点是0，非叶子节点的height往根节点递增，比如下图:

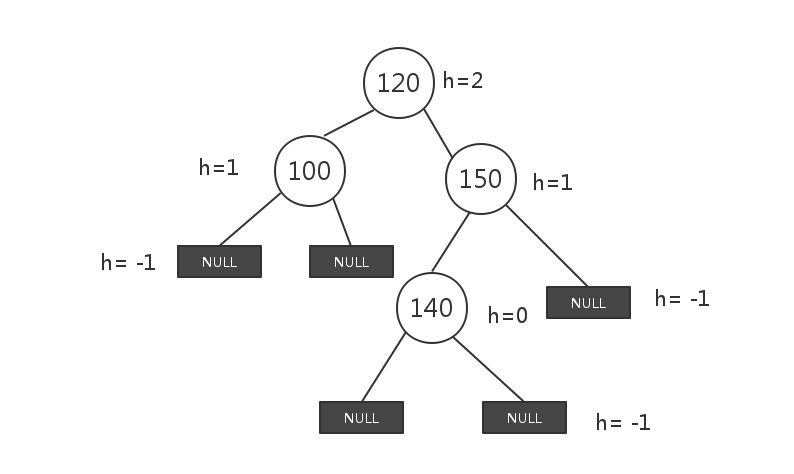
从而可得到求节点高度的方法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public static <T> int getHeight(AVLNode<T>rootNode,boolean recursionFlag){
    if(recursionFlag){
    	 if(null==rootNode){
    	    return -1;
	    }
	    int leftHeight=getHeight(rootNode.left)+1;
	    int rightHeight=getHeight(rootNode.right)+1;
	    return leftHeight>rightHeight?leftHeight:rightHeight;
    }else{
    	//由于跟深度相反，故最大深度即为高度，利用求深度的方法即可
    	if(null==rootNode){
    		return -1;
    	}
    	int currentDepth=-1;
    	int maxDepth=-1;
    	AVLNode<T>currentNode;
    	Stack<AVLNode<T>>nodeStack=new Stack<>();
    	Stack<Integer>depthStack=new Stack<>();
        nodeStack.push(rootNode);
        depthStack.push(0);
        while(!nodeStack.isEmpty()){
            currentNode=nodeStack.pop();
            currentDepth=depthStack.pop();
            if(currentDepth>maxDepth){
            	maxDepth=currentDepth;
            }
            if(currentNode.left!=null){
            	nodeStack.push(currentNode.left);
            	depthStack.push(currentDepth+1);
            }
            if(currentNode.right!=null){
            	nodeStack.push(currentNode.right);
            	depthStack.push(currentDepth+1);
            }
        }
        return maxDepth;
    } 
   
}

2.平衡操作

为了保持二叉查找树的平衡,在每次插入或删除节点时，如果失衡,就需要进行平衡操作.常见的失衡情况有以下几种:

2.1 左左情形，需要右旋

所谓左左情形,即插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致”根的左子树的高度”比”根的右子树的高度”大2,从而使二叉树失衡.
这种情况需要右旋，如下图所示:

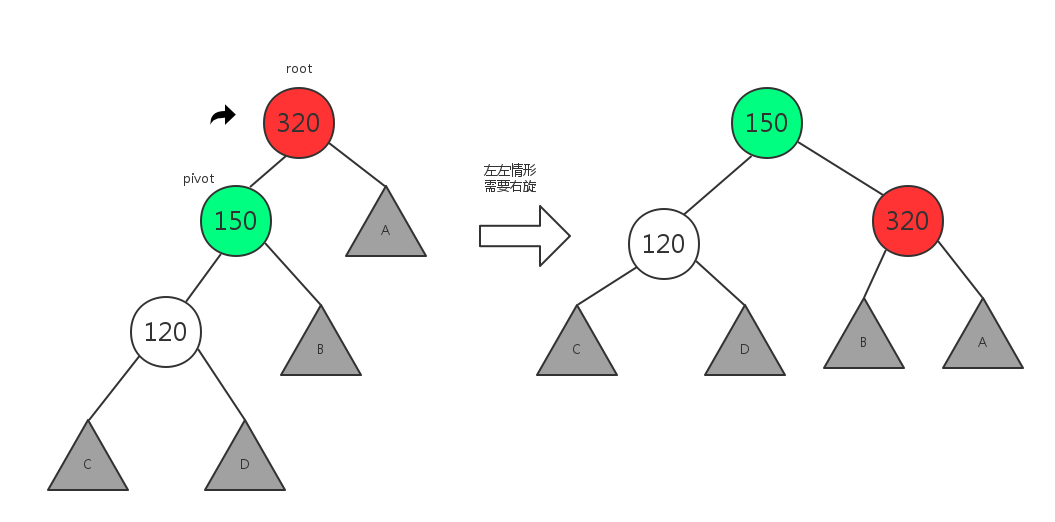
显然，右旋其实是使leftChild成为rootNode的父节点，并且rootNode成为leftChild的右孩子,附带的还有leftChild的右孩子成为rootNode的左孩子.代码如下: 

1
2
3
4
5
6
7
8
9
10
11
12
public static <T> AVLNode<T> rotateRight(AVLNode<T>rootNode){
    AVLNode<T>newTop=rootNode.left;
    rootNode.left=netTop.right;
    newTop.right=rootNode;
    //旋转结束后，需要重新求高度
    rootNode.height=getHeight(rootNode,true);
    newTop.height=getHeight(newTop,false);
    return newTop;
}

需要注意的是，虽然newTop.right的位置发生了变化，但它的height并未发生变化，故不需要重新获取它的高度.其他旋转类似.

2.2 右右情形,需要左旋

所谓右右情形,即插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致”根的右子树的高度”比”根的左子树的高度”大2,从而使二叉树失衡.
这种情况需要左旋，如下图所示:

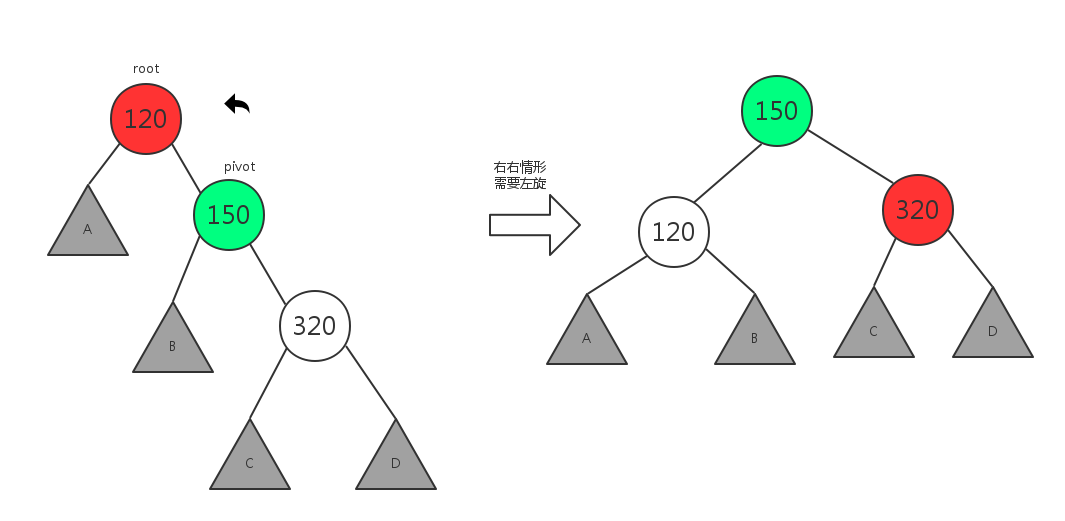
显然,左旋操作的实质是：rightChild成为rootNode的父节点，而rootNode成为rightChild的左孩子，附带操作是rightChild的左孩子成为rootNode的右孩子.代码如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static <T> AVLNode<T> rotateLeft(AVLNode<T>rootNode){
	AVLNode<T>newTop=rootNode.right;
	rootNode.right=newTop.left;
	newTop.left=rootNode;
	//determine height after rotation
	rootNode.height=getHeight(rootNode);
	newTop.height=getHeight(newTop);
	//we could also determine newTop's height with code as below:
	//newTop.height=Math.max(getHeight(top.right),rootNode.height)+1;
	return newTop;
}

2.3 左右情形,需要先左旋,然后右旋

所谓左右情形,即插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致”根的左子树的高度”比”根的右子树的高度”大2,从而使二叉树失衡.
这种情况需要先左旋，然后右旋，如下图所示:

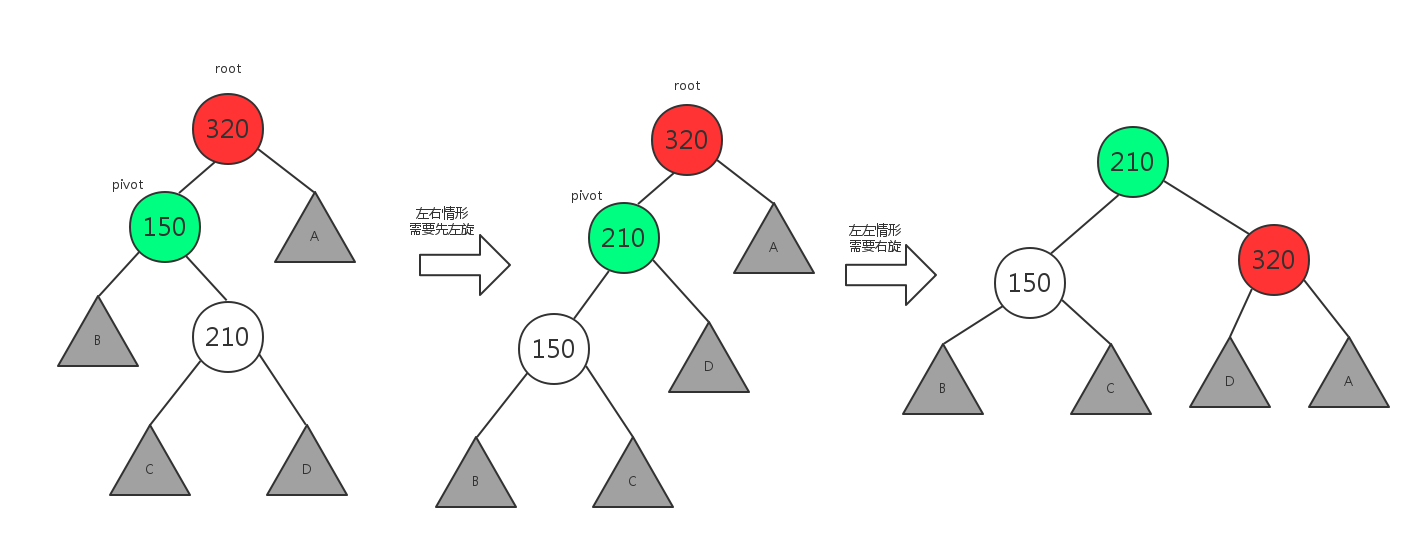
显然,左右情形只需要使用前面的左旋和右旋组合: 

1
2
3
4
5
public static <T> AVLNode<T>rotateLR(AVLNode<T>rootNode){
	AVLNode<T>newTop=rotateLeft(rootNode);
	return rotateRight(newTop);
}

2.4 右左情形,需要先右旋,然后左旋

所谓右左情形,即插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致”根的右子树的高度”比”根的左子树的高度”大2,从而使二叉树失衡.
这种情况需要先右旋，后左旋,如下图所示:

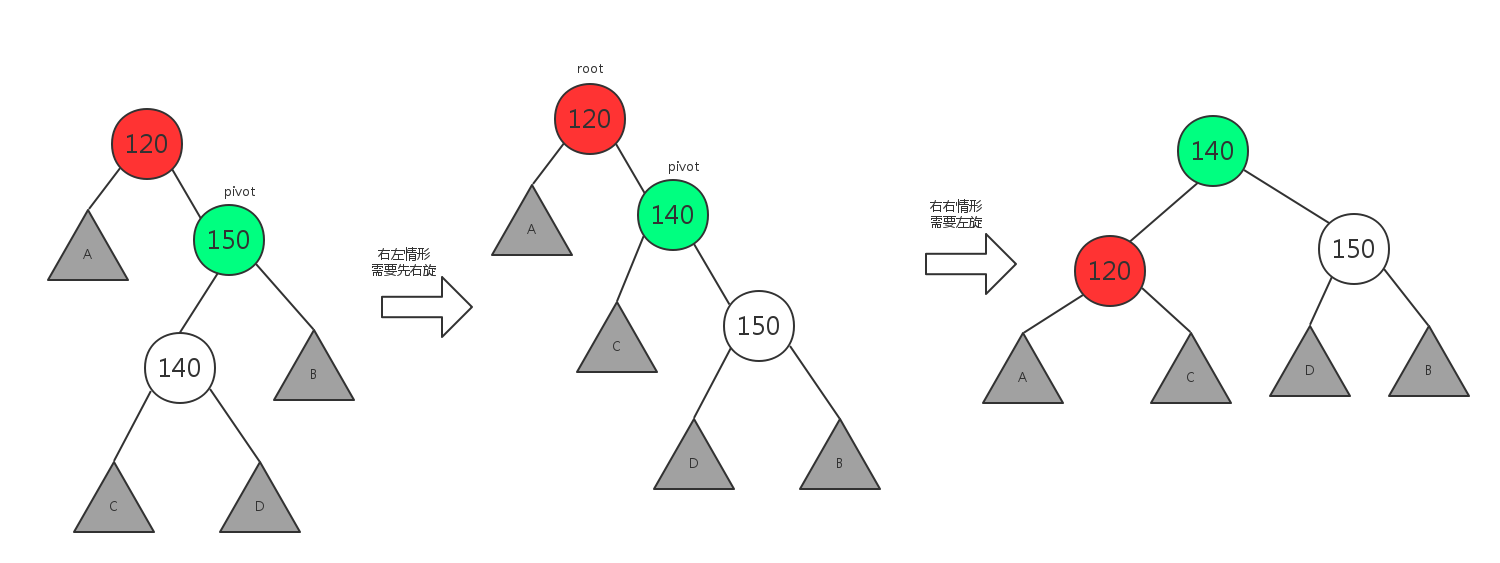
类似的，右左情形只需要使用右旋和左旋组合: 

1
2
3
4
5
public static <T> AVLNode<T>rotateRL(AVLNode<T>rootNode){
	AVLNode<T>newTop=rotateRight(rootNode);
	return rotateLeft(newTop);
}

3.插入

插入其实跟二叉查找树一样，只不过需要在每次插入结束后检查是否失衡，如失衡则需要进行相应旋转. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
private static final int FLAG_FIRST=0x1;
private static final int FLAG_SECOND=0x2;
public static <T> AVLNode<T> insert(T t,AVLNode<T>rootNode,boolean recursionFlag){
   if(recursionFlag){
   	   if(null==rootNode){
   	   	  return new AVLNode<>(t);
   	   }
   	   if(t.compareTo(rootNode.data)<0){
   	   	  rootNode.left=insert(t,rootNode.left,true);
   	   	  //插入后如果失衡
   	   	  //其实可以直接用rootNode.left.height和rootNode.right.height吧?
   	   	  if(getHeight(rootNode.left)-getHeight(rootNode.right)>=2){
   	   	  	//说明是左左情形,需要右旋 
   	   	  	if(t.compareTo(rootNode.left.data)<0){
                 rootNode=rotateRight(rootNode);
   	   	  	}else{
   	   	  		rootNode=rotateLR(rootNode);
   	   	  	}
   	   	  }
   	   }else if(t.compareTo(rootNode.data)>0){
   	   	  rootNode.right=insert(t,rootNode.right,true);
   	   	  if(getHeight(rootNode.right)-getHeight(rootNode.left)>=2){
   	   	  	  //说明是右右情形,需要左旋
   	   	  	  if(t.compareTo(rootNode.right.data)>0){
                  rootNode=rotateLeft(rootNode);
   	   	  	  }else{
   	   	  	  	  rootNode=rotateRL(rootNode);
   	   	  	  }
   	   	  }
   	   }else{
   	   	  //do nothing
   	   }
   }else{
   	   if(null==rootNode){
   	   	return new AVLNode<>(t);
   	   }
       
       //first,we need to insert.
        AVLNode<T>currentNode=rootNode;
        int result;
        while(true){
        	result=t.compareTo(currentNode.data);
        	if(result<0){
        		if(currentNode.left==null){
        			currentNode.left=new AVLNode<>(t);
        			break;
        		}else{
                    currentNode=currentNode.left;
        		}
        	}else if(result>0){
        		if(currentNode.right==null){
        			currentNode.right=new AVLNode<>(t);
        			break;
        		}else{
        			currentNode=currentNode.right;
        		}
        	}else{
        		break;
        	}
        } 
        //then we need to rebalance 
        AVLNode<T>parentNode;
       Stack<AVLNode<T>>nodeStack=new Stack<>();
       Stack<AVLNode<T>>parentNodeStack=new Stack<>();
       Stack<Integer>flagStack=new Stack<>();
       nodeStack.push(rootNode);
       flagStack.push(FLAG_FIRST);
       int flag; 
       while(!nodeStack.isEmpty()){
          currentNode=nodeStack.peek();
          flag=flagStack.peek();
          if(flag==FLAG_FIRST){
          	 flagStack.pop();
          	 flagStack.push(FLAG_SECOND);
             if(currentNode.left!=null){
             	parentNodeStack.push(currentNode);
             	nodeStack.push(currentNode.left);
             	flagStack.push(FLAG_FIRST);
             }
             if(currentNode.right!=null){
             	parentNodeStack.push(currentNode);
                nodeStack.push(currentNode.right);
                flagStack.push(FLAG_FIRST);
             }
          }else{
          	 nodeStack.pop();
          	 flagStack.pop();
          	 if(parentNodeStack.isEmpty()){
          	 	parentNode=null;
          	 }else{
          	 	parentNode=parentNodeStack.pop();
          	 }
          	 
          	 if(null!=parentNode){
          	 	if(currentNode==parentNode.left){
          	 		parentNode.left=rebalance(currentNode);
          	 	}else{
          	 		parentNode.right=rebalance(currentNode);
          	 	}
          	 }else{
          	 	rebalance(currentNode);
          	 }
          }
       }
       return rootNode;
   }
}
private static <T> AVLNode<T> rebalance(AVLNode<T>rootNode){
	if(rootNode.left==null||rootNode.right==null){
		return rootNode;
	}
	if(rootNode.left.height-rootNode.right.height>=2){
		//左左情形
		if(getLeftChildHeight(rootNode.left)>getRightChildHeight(rootNode.left)){
             return rotateRight(rootNode);
		}else{
			//左右情形
			return rotateLR(rootNode);
		}
	}else if(rootNode.right.height-rootNode.left.height>=2){
		//右右情形
		if(getRightChildHeight(rootNode.right)>getLeftChildHeight(rootNode.right)){
			return rotateLeft(rootNode);
		}else{
			return rotateRL(rootNode);
		}
	}else{
		//无需平衡，直接返回
		return rootNode;
	}
}
private static <T> int getLeftChildHeight(AVLNode<T>rootNode){
	if(rootNode.left==null){
		return -1;
	}
	return rootNode.left.height;
}
private static <T> int getRightChildHeight(AVLNode<T>rootNode){
	if(null==rootNode.right){
		return -1;
	}
	return rootNode.right.height;
}

4.删除

删除与普通的二叉查找树一样，只不过在删除节点后需要进行平衡操作. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public static <T> AVLNode<T>remove(T t,AVLNode<T>rootNode){
	if(null==rootNode){
		return null;
	}
	if(t.compareTo(rootNode.data)<0){
		rootNode.left=remove(t,rootNode.left);
        
        //right child may be deeper than left child after remove a node in left child 
		if(getHeight(rootNode.right)-getHeight(rootNode.left)>=2){
			AVLNode<T>currentNode=rootNode.right;
			if(getHeight(currentNode.left)>getHeight(currentNode.right)){
				rootNode=rotateRL(rootNode);
			}else{
				rootNode=rotateLeft(rootNode);
			}
		}
	}else if(t.compareTo(rootNode.data)>0){
		rootNode.right=remove(t,rootNode.right);
		if(getHeight(rootNode.left)-getHeight(rootNode.right)>=2){
			AVLNode<T>currentNode=rootNode.left;
			if(getHeight(currentNode.left)>getHeight(currentNode.right)){
				rootNode=rotateRight(rootNode);
			}else{
				rootNode=rotateLR(rootNode);
			}
		}
	}else{
		if(rootNode.left!=null&&rootNode.right!=null){
            
            T rightMinValue=findMin(rootNode.right).data;
            rootNode.data=rightMinValue;
            rootNode.right=remove(rightMinValue,rootNode.right); 
            
		}else{
			rootNode=rootNode.left==null?rootNode.right:rootNode.left;
			if(rootNode==null){
				return null;
			}
		}
	}
	rootNode.height=getHeight(rootNode);
	return rootNode;
}