Treap树及Java实现

引言

前面说过，二叉查找树有可能退化为链表，所以前辈们想尽了各种优化策略，包括AVL，红黑，以及今天要讲的Treap树。Treap树是一种简单的优化策略，从名字也可以猜到(Treap=Tree+Heap)，它是树和堆的合体。实原理很简单，在树中维护一个”优先级“，”优先级“采用随机数的方法生成，但是”优先级“必须满足根堆的性质，当然是“大根堆”或者“小根堆”都无所谓，比如下面的一棵树:

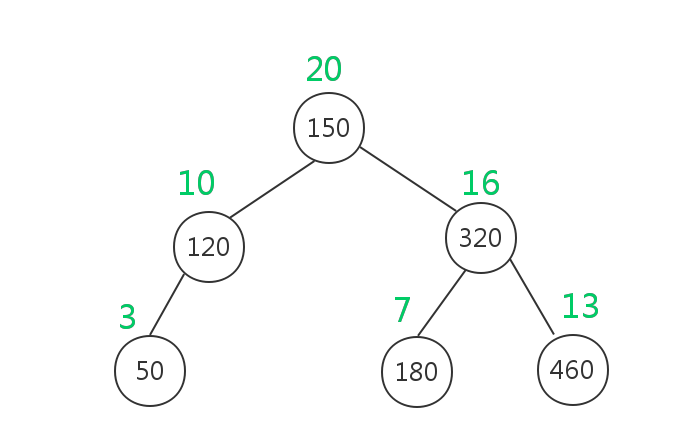
从树中我们可以看到:
1)节点中的值满足二叉查找树特性;
2)节点中的优先级满足最大堆特性;

p.s:由于采用最大和最小堆的效果一样，本文采用最大堆进行讨论。

1.定义


public class TreapNode<T> {
    public T data;
    public int priority;
    public TreapNode<T>left,right;
    public TreapNode(){}
    public TreapNode(T data,TreapNode<T>left,TreapNode<T>right){
        this.data=data;
        this.priority=new Random(System.currentTimeMillis()).nextInt(Integer.MAX_VALUE);
        this.left=left;
        this.right=right;
    }
}

2.插入节点

我们知道各个节点的优先级是采用随机数的方法，那么就存在一个问题，当我们按照二叉查找树规则插入一个节点后，优先级有可能不满足最大堆定义。显然，此时跟维护堆一样，如果当前节点的优先级比根大就旋转，如果当前节点是根的左儿子就右旋，如果当前节点是根的右儿子就左旋。如下图所示:

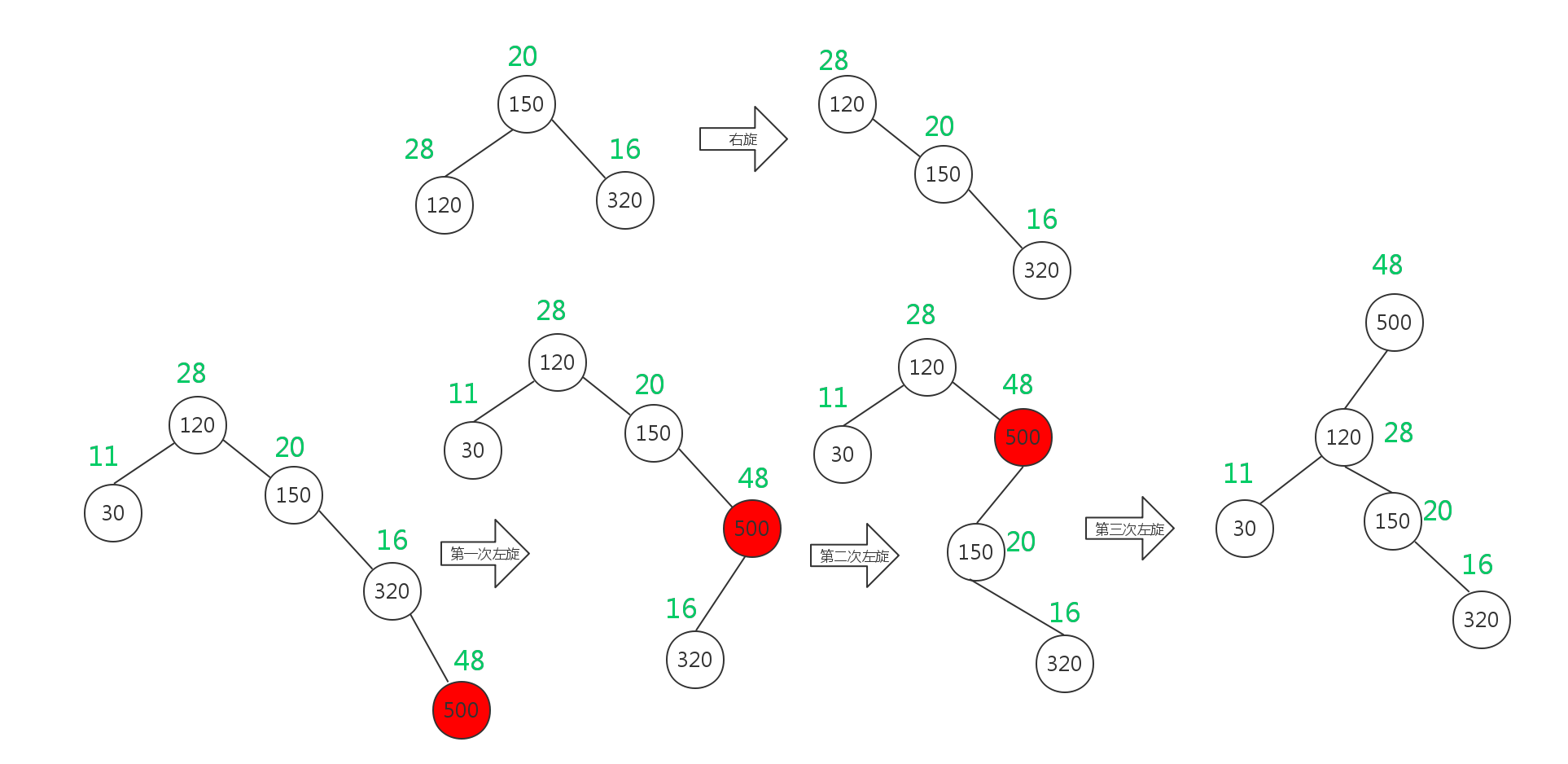
上图中右旋只展示了一次，而左旋则展示了三次递归的过程。其实理解了AVL的旋转，就能很容易理解这里的旋转了.旋转代码与AVL的完全一样.

右旋代码如下所示:

public static <T> TreapNode<T> rotateRight(TreapNode<T>rootNode){
	TreapNode<T>newTop=rootNode.left;
	rootNode.left=newTop.right;
	newTop.right=rootNode;
	rootNode.height=getHeight(rootNode,true);
	newTop.height=getHeight(newTop,false);
	return newTop;
}

左旋代码如下所示:


public static <T> TreapNode<T> rotateLeft(TreapNode<T>rootNode){
	TreapNode<T>newTop=rootNode.right;
	rootNode.right=newTop.left;
	newTop.left=rootNode;
	rootNode.height=getHeight(rootNode,true);
	newTop.height=getHeight(newTop,false);
	return newTop;
}

故插入代码如下:

public static <T> TreapNode<T> insert(T t,TreapNode<T>rootNode){
    if(null==rootNode){
    	return TreapNode<>(t,null,null);
    }
    int result=t.compareTo(rootNode.data);
    if(result<0){
    	rootNode.left=insert(t,rootNode.left);
        //根据最大堆性质，需要右旋
    	if(rootNode.left.priority>rootNode.priority){
    		rootNode=rotateRight(rootNode);
    	}
    }else if(result>0){
    	rootNode.right=insert(t,rootNode.right);
    	if(rootNode.right.priority>rootNode.priority()){
    		rootNode=rotateLeft(rootNode);
    	}
    }else{
    	//do nothing
    }
    return rootNode;
   
}

由于旋转是O(1)的，最多进行h次(h是树的高度)旋转,故插入的时间复杂度是O(lgN).

3.移除节点

跟普通的二叉查找树一样，删除结点存在三种情况。

1)叶子结点

跟普通查找树一样，直接释放本节点即可。
2)单孩子结点

跟普通查找树一样操作。
3)满孩子结点

在treap中移除满孩子结点有两种方式。第一种和普通二叉查找树一样，找到左子树的最大节点或者右子树的最小节点，然后copy元素的值，但不拷贝其优先级（以免破坏堆属性),如下图所示:

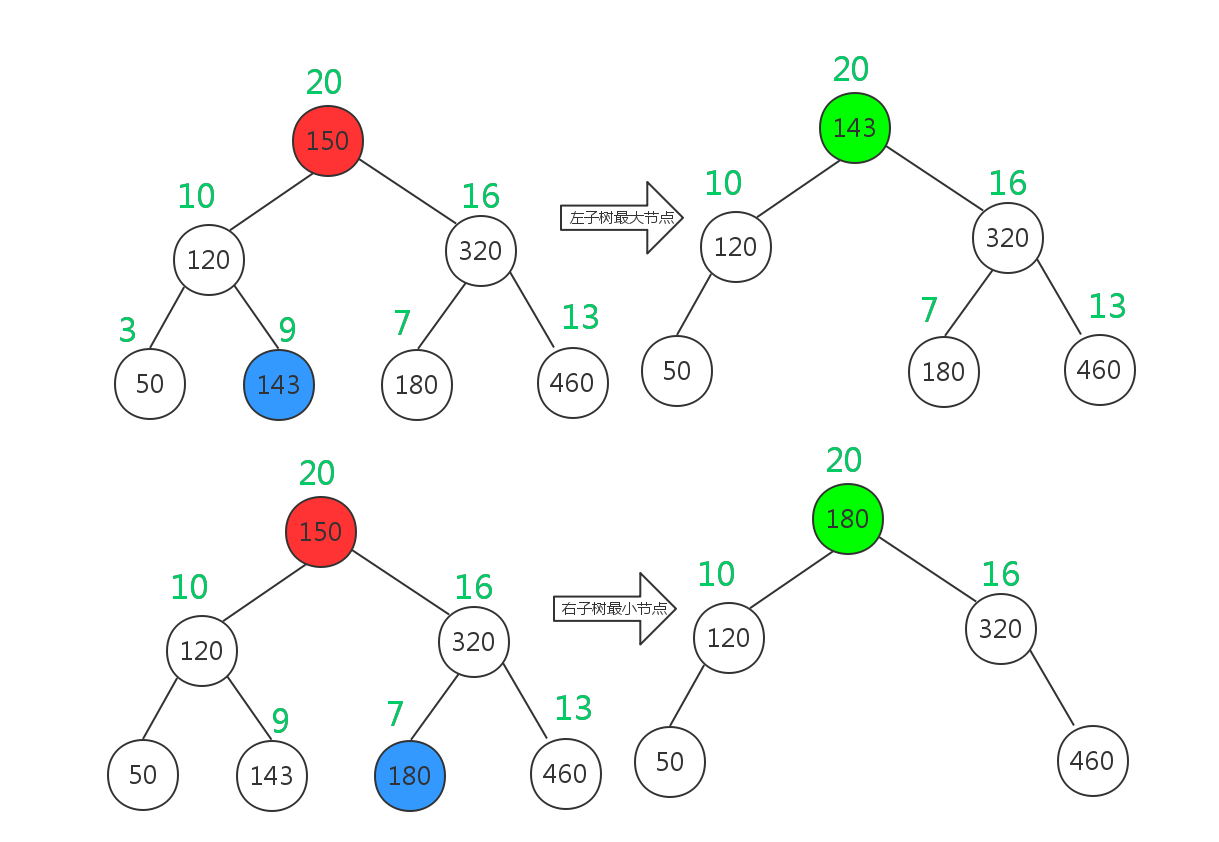
第二种是采用旋转的方法:因为Treap树满足堆性质，所以只需要把要删除的节点旋转到叶节点上，然后直接删除就可以了。具体的方法就是每次找到优先级最大的儿子，向与其相反的方向旋转，直到那个节点被旋转到了叶节点，然后直接删除。删除最多进行O(h)次旋转，期望复杂度是 O(lgN).示意图如下所示:

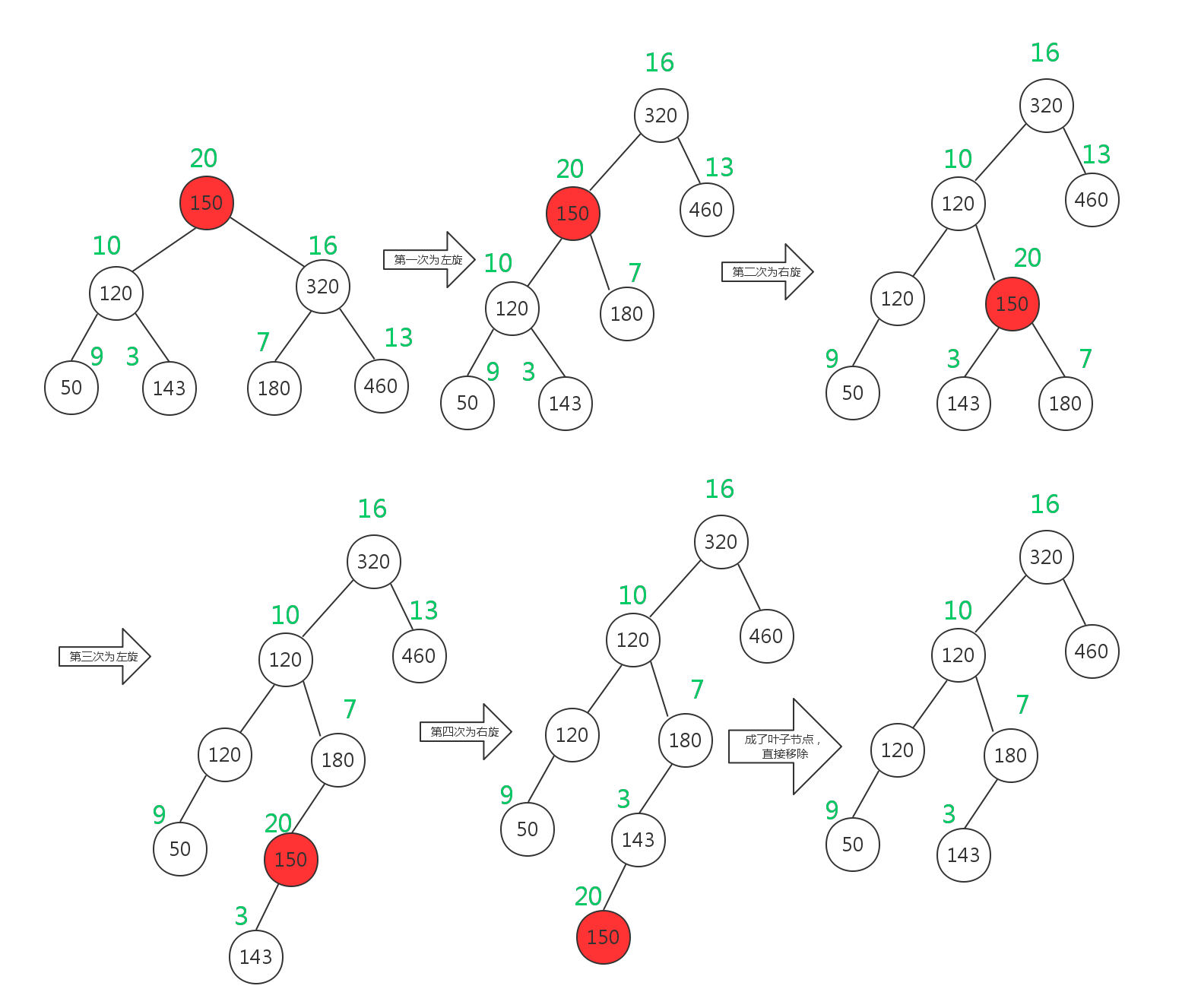
综上，移除节点的代码如下:


public static <T> TreapNode<T> remove(TreapNode<T>rootNode,T t,boolean rotateFlag){
	if(rotateFlag){
       if(null==rootNode){
       	return null;
       }
       int result=t.compareTo(rootNode.data);
       if(result<0){
       	   rootNode.left=remove(rootNode.left,t,true);
       }else if(result>0){
       	   rootNode.right=remove(rootNode.right,t,true);
       }else{
       	   if(rootNode.left!=null&&rootNode.right!=null){
       	   	   //若左孩子priority更大，则右旋
       	   	   if(rootNode.left.priority>rootNode.right.priority){
       	   	   	   rootNode=rotateRight(rootNode);
       	   	   }else{
       	   	   	    //反之左旋
       	   	   	    rootNode=rotateLeft(rootNode);
       	   	   }
               //继续旋转
               rootNode=remove(rootNode,t,true);
       	   }else{
       	   	   rootNode=rootNode.left==null?rootNode.right:rootNode.left;
       	   }
       }
       return rootNode;
	}else{
 
       if(null==rootNode){
       	   return null;
        }
        int result=t.compareTo(rootNode.data);
        if(result<0){
        	rootNode.left=remove(rootNode.left,t,false);
        }else if(result>0){
        	 rootNode.right=remove(rootNode.right,t,false);
        }else{
        	 if(rootNode.left!=null&&rootNode.right!=null){
        	 	T leftMaxValue=findMax(rootNode.left);
        	 	rootNode.data=leftMaxValue;
        	 	remove(rootNode.left,leftMaxValue,false);
        	 }else{
        	 	rootNode=rootNode.left==null?rootNode.right:rootNode.left;
        	 }
        }
        return rootNode;
    }
}

引言

1.定义

2.插入节点

3.移除节点

4.测试