伸展树及Java实现

发表于 | 分类于

引言

我们知道AVL树为了保持严格的平衡，所以在数据插入上会呈现过多的旋转，影响了插入和删除的性能。从访问量上，我们知道许多应用场景都有一个“二八原则“，也就是说80%的人只会用到20%的数据，比如说我们的用的输入法，平常打的字也就那么多，或许还没有20%呢。右比如新闻消息，热门消息的访问量是远远大于普通消息的。

所以如果让经常被访问的节点更靠近根，则平均访问速度要快很多。则就是伸展树(Splay Tree)的思想。

1.定义

伸展树(Splay Tree)是特殊的二叉查找树。它的特殊是指，它除了本身是棵二叉查找树之外，它还具备一个特点: 当某个节点被访问时，伸展树会通过旋转使该节点成为树根。这样做的好处是，下次要访问该节点时，能够迅速的访问到该节点。

这里可以使用BinaryNode，无须在定义，因为只是查询操作不一样。

1.伸展

伸展即将某个节点旋转成为根节点，而实现的方法分为“自底向上”和”自顶向下”.其中“自底向下”需要利用旋转，而”自顶向下”则除了旋转之外，还需要进行连接操作。

2.1自底向上:旋转

其实思路很简单，如果节点在左边，则进行右旋；如果节点在右边，则进行左旋。不过需要注意的是旋转过程必须是自底向上的，反过来则不行。

如下是一个典型的自底向上旋转的过程(将节点33伸展成为根节点):

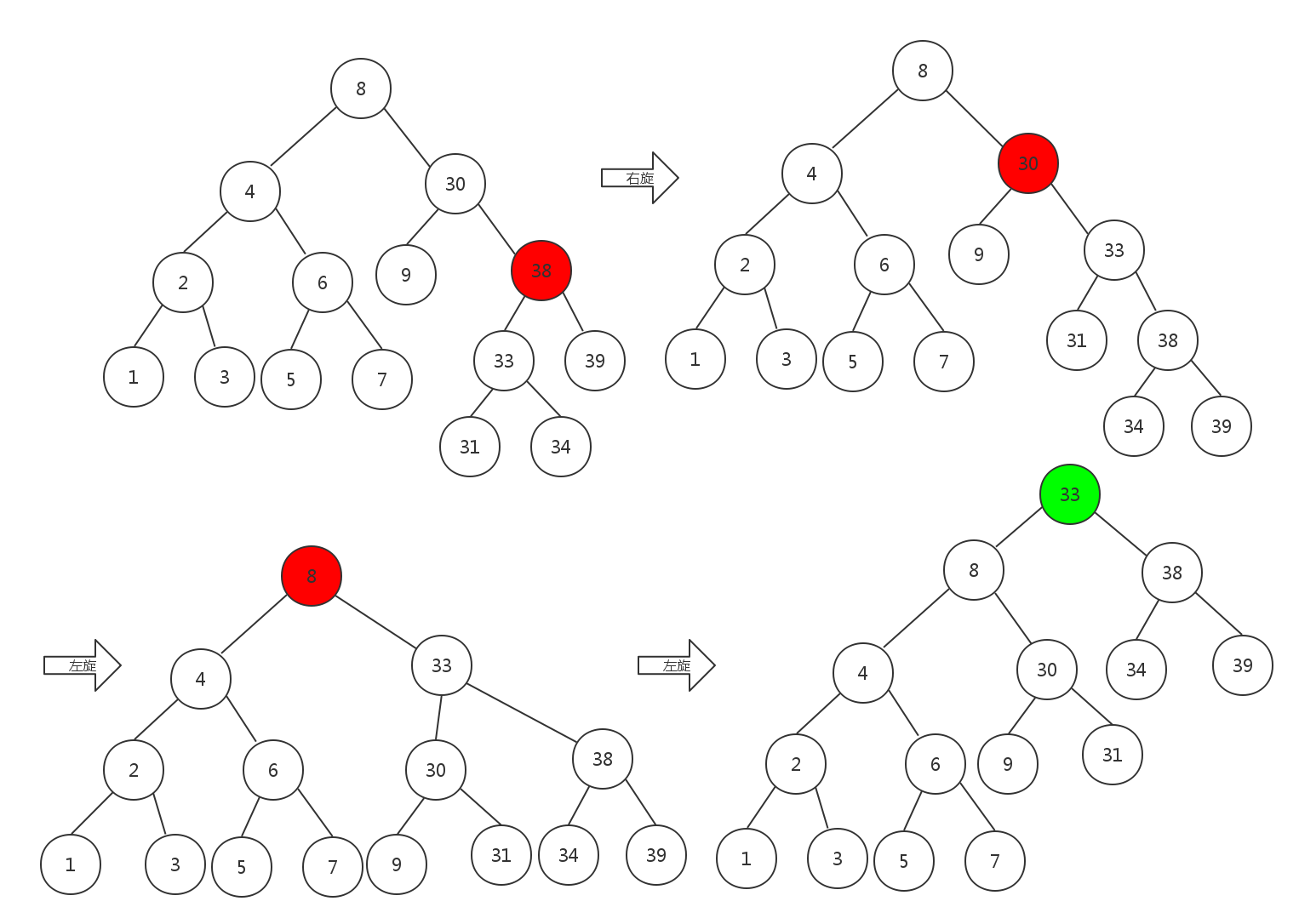
理解了这个过程，马上就能写出这个伸展的递归和非递归代码了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
/**
    * 但是这个方法只适用于节点存在的情形
    * @param rootNode
    * @param t 
    * @param recursionFlag 递归标志
    * @param <T>
    * @return
    */
   public static <T extends Comparable<T>>BinaryNode<T>splay(BinaryNode<T>rootNode,T t ,
                                                                   boolean recursionFlag){
       if(recursionFlag){
           if(null==rootNode){
               return null;
           }
           int result=t.compareTo(rootNode.data);
           if(result<0){
               rootNode.left=splayByRotation(rootNode.left,t,true);
               rootNode=rotateRight(rootNode);
           }else if(result>0){
               rootNode.right=splayByRotation(rootNode.right,t,true);
               rootNode=rotateLeft(rootNode);
           }else{
               return rootNode;
           }
           return rootNode;
       }else{
           if(null==rootNode){
               return null;
           }
           //如果只有一个节点,则无须伸展
           if(rootNode.left==null&&rootNode.right==null){
               return rootNode;
           }
           Stack<BinaryNode<T>>parentStack=new Stack<>();
           BinaryNode<T>currentNode=rootNode;
           int result;
           while(true){
               result=t.compareTo(currentNode.data);
               if(result<0){
                   if(null!=currentNode.left){
                       parentStack.push(currentNode);
                       currentNode=currentNode.left;
                   }else{
                       return rootNode;
                   }
               }else if(result>0){
                   if(null!=currentNode.right){
                       parentStack.push(currentNode);
                       currentNode=currentNode.right;
                   }else{
                       return rootNode;
                   }
               }else{
                   break;
               }
           }
           BinaryNode<T>parentNode,grandParentNode;
           while(!parentStack.isEmpty()){
               parentNode=parentStack.pop();
               if(parentStack.isEmpty()){
                   grandParentNode=null;
               }else{
                   grandParentNode=parentStack.peek();
               }
               if(parentNode.left==currentNode){
                   //then we need to rotateRight
                   if(grandParentNode!=null){
                       if(grandParentNode.left==parentNode){
                           parentNode=rotateRight(parentNode);
                           grandParentNode.left=parentNode;
                           //grandParentNode.left=rotateRight(parentNode);
                       }else{
                           parentNode=rotateRight(parentNode);
                           grandParentNode.right=parentNode;
                           //grandParentNode.right=rotateRight(parentNode);
                       }
                   }else{
                       parentNode=rotateRight(parentNode);
                   }
               }else{
                   //then we need to rotateLeft
                   if(grandParentNode!=null){
                       if(grandParentNode.left==parentNode){
                           parentNode=rotateLeft(parentNode);
                           grandParentNode.left=parentNode;
                       }else{
                           parentNode=rotateLeft(parentNode);
                           grandParentNode.right=parentNode;
                       }
                   }else{
                       parentNode=rotateLeft(parentNode);
                   }
               }
               currentNode=parentNode;
           }
           rootNode=currentNode;
           return rootNode;
       }
   }

递归代码非常简洁，非递归的思想也是一样的，只不过利用parentStack来达到自底向上的效果。

2.2 自顶向下:利用L,M,R树

思想就是如果目标节点在右孩子中，则将右子树保留在M中，其余部分与之前的L树融合;如果目标节点在左孩子中，则将左子树保留在M中，其余部分与之前的R树融合.一直循环直到找到节点，然后将目标节点的左子树与L树融合，右子树与R树融合。最后将使M.left=L,M.right=R即可。

如下是一个典型的自顶向下的分裂过程。

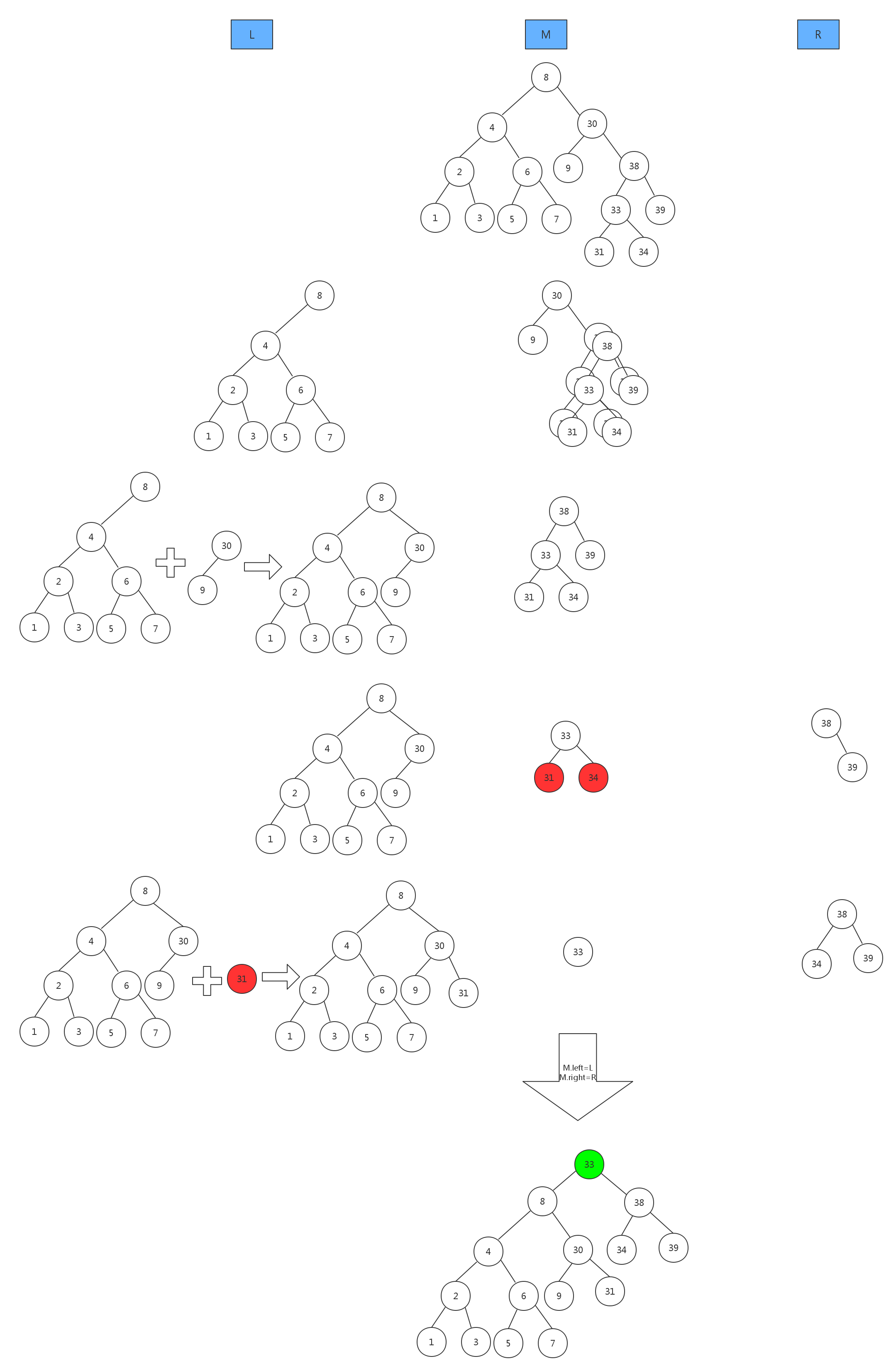
代码如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public static <T extends Comparable<T>> BinayNode<T> splayBySplit(BinayNode<T>rootNode,T t){
   if(null==rootNode){
   	 return null;
   }
   BinaryNode<T>leftTree,middleTree,rightTree,tempNode;
   middleTree=rootNode;
   int result;
   while(true){
      result=t.compareTo(middleTree.data);
      if(result<0){
         //split and put right child into rightTree
         tempNode=middleTree;
         middleTree=tempNode.left;
         tempNode.left=null;
         rightTree=SearchTree.insert(rightTree,tempNode);  
      }else if(result>0){
      	//split and push left child into leftTree
         tempNode=middleTree;
         middleTree=tempNode.right;
         tempNode.right=null;
         leftTree=SearchTree.insert(leftTree,tempNode);
      }else{
         leftTree=SearchTree.insert(leftTree,middleTree.left);
         rightTree=SearchTree.insert(rightTree,middleTree.right);
         middleTree.left=leftTree;
         middleTree.right=rightTree; 
      	 break;
      }
   }
   return middleTree;
}

上面两种算法很简洁，也很好理解，但是有一个不足之处是只适应于节点一定存在的场合。但是完整的伸展过程应该是:

  • (a)：伸展树中存在”键值为key的节点”。 
    将"键值为key的节点"旋转为根节点。
  • (b)：伸展树中不存在”键值为key的节点”，并且key < tree.key。 
    b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。  
b-2 "键值为key的节点"的前驱节点不存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
  • (c)：伸展树中不存在”键值为key的节点”，并且key > tree.key 
    c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。  
c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。

对应的代码为: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
private SplayTreeNode<T> splay(SplayTreeNode<T> tree, T key) {
    if (tree == null) 
        return tree;
    SplayTreeNode<T> N = new SplayTreeNode<T>();
    SplayTreeNode<T> l = N;
    SplayTreeNode<T> r = N;
    SplayTreeNode<T> c;
    for (;;) {
        int cmp = key.compareTo(tree.key);
        if (cmp < 0) {
            if (tree.left == null)
                break;
            if (key.compareTo(tree.left.key) < 0) {
                c = tree.left;                           /* rotate right */
                tree.left = c.right;
                c.right = tree;
                tree = c;
                if (tree.left == null) 
                    break;
            }
            r.left = tree;                               /* link right */
            r = tree;
            tree = tree.left;
        } else if (cmp > 0) {
            if (tree.right == null) 
                break;
            if (key.compareTo(tree.right.key) > 0) {
                c = tree.right;                          /* rotate left */
                tree.right = c.left;
                c.left = tree;
                tree = c;
                if (tree.right == null) 
                    break;
            }
            l.right = tree;                              /* link left */
            l = tree;
            tree = tree.right;
        } else {
            break;
        }
    }
    l.right = tree.left;                                /* assemble */
    r.left = tree.right;
    tree.left = N.right;
    tree.right = N.left;
    return tree;
}
public void splay(T key) {
    mRoot = splay(mRoot, key);
}

不过抱歉我花了半天时间还是没有完全理解这个算法的原理，所以就不详细分析这种了。

3.插入

插入节点的代码非常简单，只需要在普通二叉查找树的插入基础上，在加上伸展即可。 

1
2
3
4
5
6
7
public void insert(T t){
   root=SearchTree.insert(root,t);
   root=splay(root,t);
}

4.删除

它会先在伸展树中查找键值为key的节点。若没有找到的话，则直接返回。若找到的话，则将该节点旋转为根节点，然后再删除该节点，之后将它的前驱节点作为根节点；如果它的前驱节点不存在，则根为它的右孩子。

如果使用2.2.2的伸展方法，则删除节点的代码比较简单: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
   * 删除节点，返回被删除的节点
   * @param t
   * @return
   */
  public BinaryNode<T> remove(T t){
      BinaryNode<T>newRoot,removedNode;
      if(null==root){
          return null;
      }
      removedNode=SearchTree.search(root,t);
      if(removedNode==null){
          return null;
      }
      root=splay(root,t);
      if(root.left!=null){
          // 将"tree的前驱节点"旋转为根节点
          newRoot=splay(root.left,t);
          newRoot.right=root.right;
      }else{
          newRoot=root.right;
      }
      root=newRoot;
      return removedNode;
  }

如果使用自己的算法，其实也只是多了一步寻找前驱节点的过程。代码如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public BinaryNode<T> remove(T t){
    BinaryNode<T>newRoot,removedNode;
    if(null==root){
    	return null;
    }
    removedNode=SearchTree.search(root,t);
    if(removedNode==null){
    	return null;
    }
    root=splay(root,t);
    if(root.left!=null){
    	BinaryNode<T>predecessor=SearchTree.findPredessor(root,true);
    	newRoot=splay(root.left,predecessor.data);
    	newRoot.right=root.right;
    }else{
    	newRoot=root.right;
    }
    root=newRoot;
    return removedNode;
}

5.测试