Huffman树及Java实现

发表于 | 分类于

引言

霍夫曼编码（英语：Huffman Coding），又译为哈夫曼编码、赫夫曼编码，是一种用于无损数据压缩的熵编码（权编码）算法。由大卫·霍夫曼在1952年发明。
在计算机数据处理中，霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现概率的方法得到的，出现概率高的字母使用较短的编码，反之出现概率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

例如，在英文中，e的出现概率最高，而z的出现概率则最低。当利用霍夫曼编码对一篇英文进行压缩时，e极有可能用一个比特来表示，而z则可能花去25个比特（不是26）。用普通的表示方法时，每个英文字母均占用一个字节，即8个比特。二者相比，e使用了一般编码的1/8的长度，z则使用了3倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算，就可以大幅度提高无损压缩的比例。

霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1L1+W2L2+W3L3+…+WnLn），N个权值Wi（i=1,2,…n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,…n）。可以证明霍夫曼树的WPL是最小的。

如下的两棵树都是以{10, 20, 50, 100}为叶子节点的树：

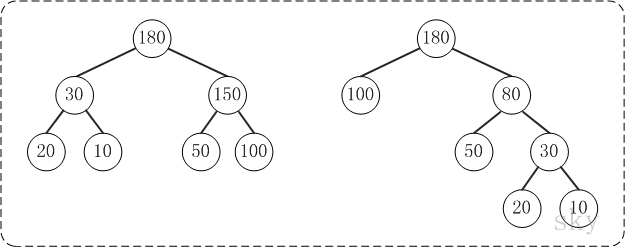
显然:
左边的树WPL=210 + 220 + 250 + 2100 = 360
右边的树WPL=350

而Huffman树就是要针对某些字符，构造出最优的二叉树。

1.定义

代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class HuffNode implements Comparable<HuffNode>{
    public char data;
    public int weight;
    public HuffNode left;
    public HuffNode right;
    public HuffNode parent;
    public HuffNode() {
    }
    public HuffNode(char data, int weight) {
        this.data = data;
        this.weight = weight;
    }
    @Override
    public int compareTo(HuffNode another) {
        return weight < another.weight ? -1 : (weight == another.weight ? 0 : 1);
    }
}

Huffman树的定义如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class HuffTree {
    private static final char DUMMY_DATA = '*';
    private static final char LEFT_FLAG = '0';
    private static final char RIGHT_FLAG = '1';
    private HuffNode root;
    private List<HuffNode> leafNodes = new ArrayList<>();
    public HuffTree() {
    }
    ...
}

2.构造

如下一副图来自维基，很形象地显示了Huffman树的构造过程:

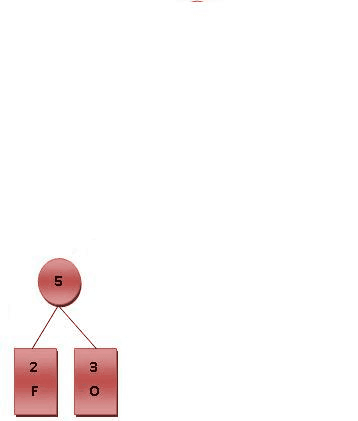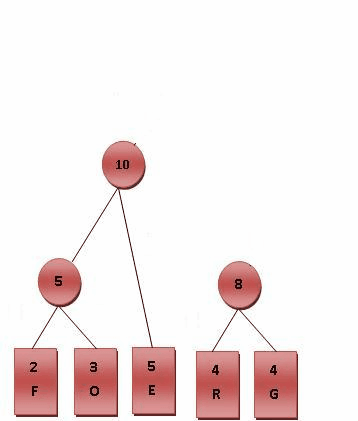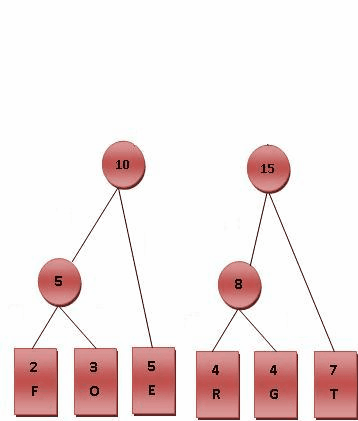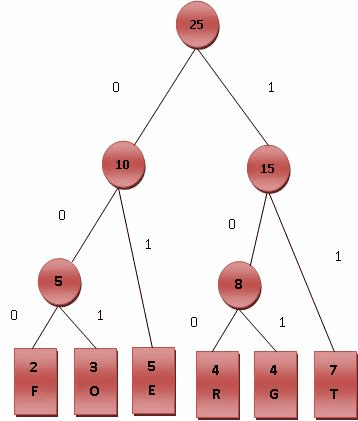
以下引用自维基:
实现霍夫曼树的方式有很多种，可以使用优先队列（Priority Queue）简单达成这个过程，给与权重较低的符号较高的优先级（Priority），算法如下：

  • ⒈把n个终端节点加入优先队列，则n个节点都有一个优先权Pi，1 ≤ i ≤ N
  • ⒉如果队列内的节点数>1，则：
  • ⑴从队列中移除两个最大的Pi节点，即连续做两次remove（max(Pi）, Priority_Queue)
  • ⑵产生一个新节点，此节点为（1）之移除节点之父节点，而此节点的权重值为（1）两节点之权重和
  • ⑶把（2）产生之节点加入优先队列中
  • ⒊最后在优先队列里的点为树的根节点（root）
    而此算法的时间复杂度（ Time Complexity）为O(NlgN)；因为有N个终端节点，所以树总共有2N-1个节点，使用优先队列每个循环须O(lgN)。
    此外，有一个更快的方式使时间复杂度降至线性时间（Linear Time）O(N)，就是使用两个队列（Queue）创件霍夫曼树。第一个队列用来存储n个符号（即n个终端节点）的权重，第二个队列用来存储两两权重的合（即非终端节点）。此法可保证第二个队列的前端（Front）权重永远都是最小值，且方法如下：
  • ⒈把n个终端节点加入第一个队列（依照权重大小排列，最小在前端）
  • ⒉如果队列内的节点数>1，则：
  • ⑴从队列前端移除两个最低权重的节点
  • ⑵将（1）中移除的两个节点权重相加合成一个新节点
  • ⑶加入第二个队列
  • ⒊最后在第一个队列的节点为根节点
    虽然使用此方法比使用优先队列的时间复杂度还低，但是注意此法的第1项，节点必须依照权重大小加入队列中，如果节点加入顺序不按大小，则需要经过排序，则至少花了O(NlgN)的时间复杂度计算。
    但是在不同的状况考量下，时间复杂度并非是最重要的，如果我们今天考虑英文字母的出现频率，变量n就是英文字母的26个字母，则使用哪一种算法时间复杂度都不会影响很大，因为n不是一笔庞大的数字。

这里采用第一种方法来实现，代码如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public static HuffNode buildTree(char[] charArray, int[] weightArray, List<HuffNode> leafNodes) {
        PriorityQueue<HuffNode> priorityQueue = new PriorityQueue<>();
        for (int i = 0; i < charArray.length; ++i) {
            HuffNode node = new HuffNode(charArray[i], weightArray[i]);
            priorityQueue.offer(node);
            leafNodes.add(node);
        }
        while (priorityQueue.size() > 1) {
            HuffNode node1 = priorityQueue.poll();
            HuffNode node2 = priorityQueue.poll();
            HuffNode sumNode = new HuffNode();
            sumNode.weight = node1.weight + node2.weight;
            sumNode.data = DUMMY_DATA;
            sumNode.left = node1;
            sumNode.right = node2;
            node1.parent = sumNode;
            node2.parent = sumNode;
            priorityQueue.offer(sumNode);
        }
        //the last one in priorityQueue is the root
        return priorityQueue.poll();
    }

3.编码

编码其实就是将路径转换为字符串，一般左孩子对应’0’,右孩子对应’1’;故采用parent节点不断溯源即可，最后利用Stack反转级得到从根节点到对应叶子节点的编码。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public List<String>encode(){
        return encode(leafNodes);
 }
  public static List<String> encode(List<HuffNode> leafNodes) {
        if (null == leafNodes || leafNodes.isEmpty()) {
            return null;
        }
        List<String> list = new ArrayList<>();
        Stack<Character> stack = new Stack<>();
        for (HuffNode node : leafNodes) {
            do {
                if (node == node.parent.left) {
                    stack.push(LEFT_FLAG);
                } else {
                    stack.push(RIGHT_FLAG);
                }
                node = node.parent;
            } while (node != null&&node.parent!=null);
            StringBuilder sb = new StringBuilder();
            while (!stack.isEmpty()) {
                sb.append(stack.pop());
            }
            list.add(sb.toString());
        }
        return list;
  }

4.解码

解码即根据编码字符串获取对应的字符. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public char decode(String codeStr){
       return decode(root,codeStr);
   }
public static char decode(HuffNode rootNode, String codeStr) {
    if (null == codeStr || null == rootNode) {
           return '\0';
       }
     char[] codeArray = codeStr.toCharArray();
     HuffNode currentNode = rootNode;
     for (char code : codeArray) {
          if (code == LEFT_FLAG) {
              currentNode = currentNode.left;
          } else {
              currentNode = currentNode.right;
          }
      }
      return currentNode.data;      
}

5.测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 HuffTree huffTree = new HuffTree();
 char[] charArray = "forget".toCharArray();
 int[] weightArray = {2, 3, 4, 4, 5, 7};
 huffTree.buildTree(charArray, weightArray);
 PrintUtils.print("Huffman tree is as follows:\n");
 PrintUtils.printAsHorizontalTreeShape(huffTree.getRoot());
 PrintUtils.reallyStartPrint();
List<String>codeList=huffTree.encode();
for(String code:codeList){
     PrintUtils.print(code+"-->"+huffTree.decode(code)+" ");
 }
PrintUtils.reallyStartPrint();

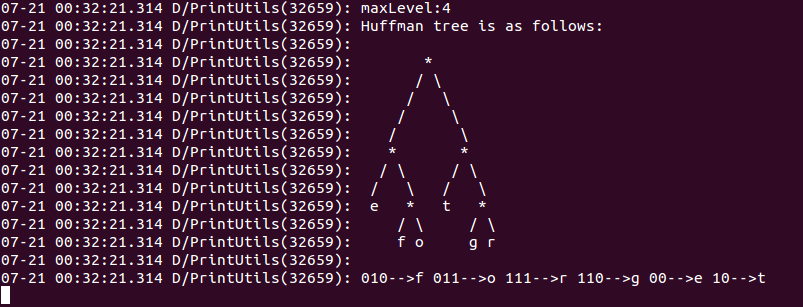
测试结果如下: