图的定义及基本操作

发表于 | 分类于

引言

图是由顶点的非空集合V和边的集合E构成的，可表示为 G=(V,E). 若图的每一条边都是无方向的，则称为无向图，反之为有向图。
图的应用非常广泛，如电子线路分析,工程计划分析，寻找最短路径，甚至估算互联网的直径。

1.基本概念

1)度

顶点的度是指依附于某顶点v的边数，通常记为TD(v);

2)路径

在无向图G中，若存在顶点序列v1,v2,…,vm使得顶点偶对(vi,vi+1)属于E,则称该顶点序列为顶点v1和vm之间的一条路径。
对于带权图，路径长度是指路径上所有边上的权值之和。
称v1=vm的路径为回路或环，序列中顶点不重复出现的路径为简单路径。
除第一个顶点和最后一个顶点之外，其他顶点不重复出现的回路称为简单回路，或者简单环。

3)图的连通

对于无向图，若从顶点vi到vj(i!=j)有路径，则称vi和vj之间是连通的。如果无向图中任意两个顶点vi和vj都是连通的，则称该无向图无连通图，否则，则称该无向图为非连通图。
无向图中的极大连通子图称为该图的连通分量。

4)生成树

若图G为包含n个顶点的连通图，则所谓G的生成树是G中包含其全部顶点的一个极小连通子图，并且该子图一定包含且仅仅包含G的n-1条边。

最后，有一个非常重要的结论:如果一个图有n个顶点和少于n-1条边，则该图一定是非连通图。如果边数多于n-1条，则图中一定存在回路。

2.图的存储

图的存储方法非常多，但无论采用什么方法，目标总是相同的，即不仅要存储图中各个顶点本身的数据信息，同时还需要存储顶点与顶点之间的所有关系的信息，如果图是带权的，还需要考虑权值的存储。
目前常用的图的存储方法主要有邻接矩阵和邻接表。

1)邻接矩阵

邻接矩阵存储其实就是数组存储，即使用一维数组存储顶点信息，二维数组存储边的信息，该二维数组即被称为邻接矩阵。

A[i][j]表示顶点i和j之间的关系时，则: 

if(Vi与Vj之间有边时){
    A[i][j]=1;
}else{
    A[i][j]=0;
}

对于网络，有: 

if(Vi与Vj之间有边时){
    A[i][j]=Wij
}else{
    A[i][j]=Integer.MAX_VALUE;
}

如下图所示的两个图，其邻接矩阵分别为：

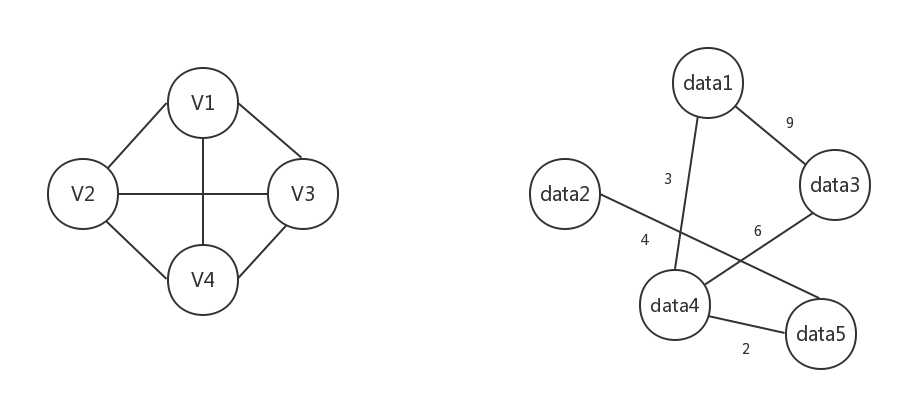
图2-1 

1
2
3
int[][]A1={ {0,1,1,1},{1,0,1,1},{1,1,0,1},{1,1,1,0} };  
int[][]A2={ {MAX,MAX,9,3,MAX},{MAX,MAX,MAX,MAX,4},{9,MAX,MAX,6,MAX},{3,MAX,6,MAX,2},{MAX,4,MAX,2,MAX} };

其中MAX为Integer.MAX_VALUE;

显然，采用邻接矩阵的存储方法具有以下特点:

  • 1)无向图的邻接矩阵一定是一个对称矩阵，因而压缩存储时只需存储上三角或下三角的元素即可;
  • 2)采用邻接矩阵时，很容易确定图中任意两个顶点之间是否存在边相连，但如果要确定图中具体有多少条边，则必须按行、按列遍历，时间复杂度为O(n^2);
  • 3)对于具有n个顶点的图采用邻接矩阵方法，空间复杂度为O(n^2)。此方法比较适合于稠密图的存储，而对于稀疏图，则势必造成存储空间的浪费;

如下是一个Graph的定义: 

1
2
3
4
5
6
7
8
9
10
11
12
public class Graph<T>{
	public T[]vertexArray;
	public int[,]adjArray;
	public int edgeNum;
	public Graph(int vertexNum,int edgeNum){
		this.vertexArray=new T[vertexNum];
		this.adjArray=new int[vertexNum,vertexNum];
		this.edgeNum=edgeNum;
	}
}

如下是一个Graph的建立过程: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static Graph<String> buildGraph(){
  String[]content={"A","B","C","D","E","F"};
  Graph<String>graph=new Graph<>(6,8);
 
  for(int i=0;i<graph.vertexArray.length;++i){
  	graph.vertexArray[i]=content[i];
  	for(int j=0;j<graph.vertexArray.length;++i){
  		graph.edges[i,j]=Integer.MAX_VALUE;
  	}
  }
  graph.adjArray[0,1]=graph.adjArray[1,0]=80;
  graph.adjArray[0,3]=graph.adjArray[3,0]=100;
  graph.adjArray[0,5]=graph.adjArray[5,0]=20;
  graph.adjArray[1,2]=graph.adjArray[2,1]=90;
  graph.adjArray[2,5]=graph.adjArray[5,2]=70;
  graph.adjArray[3,2]=graph.adjArray[2,3]=100;
  graph.adjArray[4,5]=graph.adjArray[5,4]=40;
  graph.adjArray[3,4]=graph.adjArray[4,3]=60;
  graph.adjArray[2,3]=graph.adjArray[3,2]=10;
  return graph;
}

2)邻接表

前面提到，对于稀疏图，使用邻接矩阵存储会造成空间浪费，而实际中经常遇到的都是稀疏图。对于这个问题，需要采用邻接表存储。

图的邻接表存储方法是一种顺序分配与链式分配相结合的存储方法。其中数组用于存放顶点信息，链表用于存放边的信息。

图2-1对应的邻接表如下图：

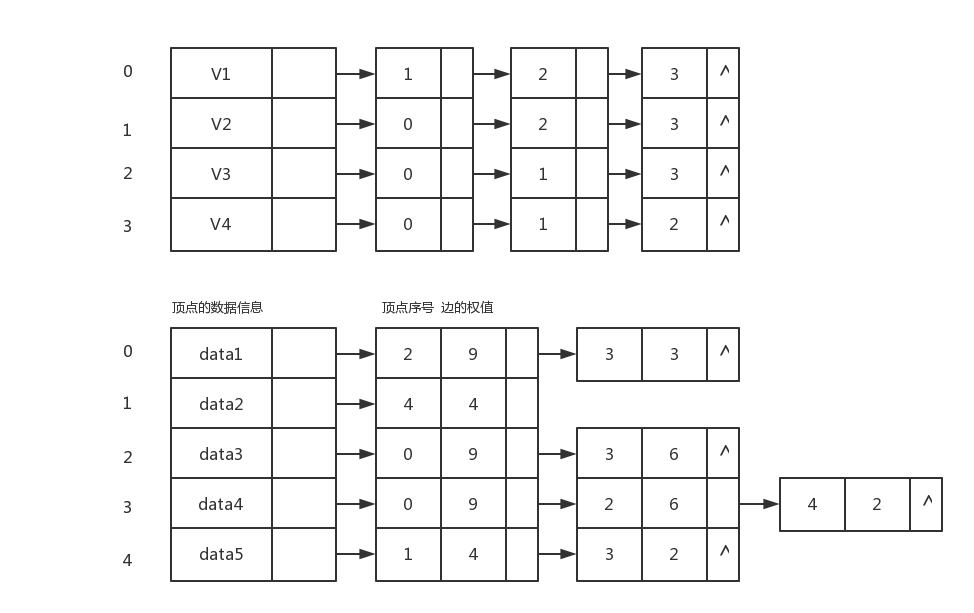
边的定义如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
public class Edge {
    //该边的终止顶点序号
    public int adjVexPos;
    public int weight;
    public Edge next;
    public Edge(){}
    public Edge(int adjVex,int weight){
        this.adjVexPos=adjVex;
        this.weight=weight;
    }
}

顶点的定义如下: 

1
2
3
4
5
public class Vertex<T> {
    public T data;
    //该顶点指向的第一条边
    public Edge edgeLink;
}

显然，此时图其实就是一个顶点数组。

3.基本操作

1)创建邻接表

如果想要通过输入数值来创建图，则可使用以下方法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public static <T> Vertex<T>[]createAdjList(int vertexNum,int edgeNum){
     Vertex<T>[]graph=new Vertex[vertexNum];
     for(int i=0;i<vertexNum;++i){
         graph[i]=new Vertex<>();
         graph[i].data=getData(i);
         graph[i].edgeLink=null;
     }
     for(int i=0;i<edgeNum;++i){
         int vertexStart=getVertexStart(i);
         int vertexEnd=getVertexEnd(i);
         Edge edge=new Edge(vertexEnd,getWeight(i));
         if(graph[vertexStart].edgeLink==null){
             graph[vertexStart].edgeLink=edge;
         }else{
             Edge currentEdge=graph[vertexStart].edgeLink;
             while(currentEdge.next!=null){
                 currentEdge=currentEdge.next;
             }
             currentEdge.next=edge;
         }
     }
     return graph;
 }

其中getVertexStart(),getVertexEnd()和getWeight()方法中需要输入数值。

显然这种方法不方便，实际上，通过邻接矩阵来创建邻接表比较常用,方法如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public static <T> Vertex<T>[]createAdjList(T[]vertexDataArray,int[][]adjArray){
    if(null==vertexDataArray||null==adjArray){
        return null;
    }
     Vertex<T>[]graph=new Vertex[vertexDataArray.length];
     for(int i=0;i<vertexDataArray.length;++i){
         graph[i]=new Vertex<>();
         graph[i].data=vertexDataArray[i];
         graph[i].edgeLink=null;
     }
     for(int i=0;i<vertexDataArray.length;++i){
         for(int j=0;j<vertexDataArray.length;++j){
             //vi,vj-->edge
             if(adjArray[i][j]==Integer.MAX_VALUE){
                 continue;
             }else{
                 Edge edge=new Edge(j,adjArray[i][j]);
                 if(graph[i].edgeLink==null){
                     graph[i].edgeLink=edge;
                 }else{
                     Edge temp=graph[i].edgeLink;
                     while(temp.next!=null){
                         temp=temp.next;
                     }
                     temp.next=edge;
                 }
             }
         }
     }
     return graph;
 }

2)删除节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public static <T> void deleteVertex(Vertex<T>[]graph,T item){
       int k=-1;
       for(int i=0;i<graph.length;++i){
           if(graph[i].data==item){
               k=i;
               break;
           }
       }
       
       if(k==-1){
           return;
       }
       for(int i=k+1;i<graph.length;++i){
           graph[i-1].data=graph[i].data;
           graph[i-1].edgeLink=graph[i].edgeLink;
       }
       int currentLength=graph.length-1;
       Edge temp,q=null;
       for(int i=0;i<currentLength;++i){
           temp=graph[i].edgeLink;
           while(temp!=null){
               if(temp.adjVexPos==k){
                 if(graph[i].edgeLink==temp){
                     graph[i].edgeLink=temp.next;
                 }else{
                     q.next=temp.next;
                 }
                 temp=temp.next;  
               }else{
                   if(temp.adjVexPos>k){
                       temp.adjVexPos--;
                   }
                   q=temp;
                   temp=temp.next;
               }
               
           }
       }
   }

3)深度优先搜索

从图中某一顶点v出发，先访问v,然后从该顶点的未被访问过的邻接点w出发进行深度优先搜索，直到图中与v相通的所有顶点都被访问。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static <T> void depthFirstSearch(Vertex<T>[]graph){
       if(null==graph){
           return;
       }
       int[]visitArray=new int[graph.length];
       for(int i=0;i<graph.length;++i){
           visitArray[i]=0;
       }
       for(int i=0;i<graph.length;++i){
           dfs(graph,visitArray,i);
       }
   }
   
   /**
   *单个节点的邻接点遍历
   */
   private static <T> void dfs(Vertex<T>[]graph,int[]visitedArray,int pos){
       print(graph[pos].data);
       visitedArray[pos]=1;
       Edge temp=graph[pos].edgeLink;
       while(temp!=null){
           if(visitedArray[temp.adjVexPos]==0){
               dfs(graph,visitedArray,temp.adjVexPos);
           }
           temp=temp.next;
       }
   }

4)广度优先搜索

从图中某一点v出发，访问v后再依次访问v的各个未被访问过的邻接点，然后从这些邻接点出发，按照同样的原则依次遍历它们的未被访问的顶点.

广度优先搜索与深度优先搜索不同，它首先访问指定出发顶点，然后依次访问该顶点的所有未被访问过的邻接点，在接下来访问邻接点的未被访问过的节点. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public static <T> void breadthFirstSearch(Vertex<T>[]graph){
        if(null==graph){
            return;
        }
        
        int[]visitedArray=new int[graph.length];
        for(int i=0;i<graph.length;++i){
            visitedArray[i]=0;
        }
        for(int i=0;i<graph.length;++i){
            if(visitedArray[i]==0){
                bfs(graph,i,visitedArray);
            }
        }
        
    }
    private static <T> void bfs(Vertex<T>[]graph, int pos,int[]visitedArray){
        print(graph[pos].data);
        visitedArray[pos]=1;
        Queue<Vertex<T>>queue=new LinkedBlockingDeque<>(5);
        queue.offer(graph[pos]);
        Vertex<T>currentVer;
        while(!queue.isEmpty()){
            currentVer=queue.poll();
            Edge edge=currentVer.edgeLink;
            while(edge!=null){
                if(visitedArray[edge.adjVexPos]==0){
                    print(graph[edge.adjVexPos].data);
                    queue.offer(graph[edge.adjVexPos]);
                    visitedArray[edge.adjVexPos]=1;
                }
                edge=edge.next;
            }
        }
    }